Question 61442This question is from textbook Calculus for the Managerial, Life, and Social Sciences
: A rectangular box is to have a square base and a volume of 20 feet cubed. If the material for the base costs $.30/square foot, the material for the sides costs $.10/square foot, and the material for the top costs $.20/square foot, determine the dimensions of the box that can be constructed at minimun cost.
This question is from textbook Calculus for the Managerial, Life, and Social Sciences
Found 2 solutions by ankor@dixie-net.com, josmiceli:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A rectangular box is to have a square base and a volume of 20 feet cubed. If the material for the base costs $.30/square foot, the material for the sides costs $.10/square foot, and the material for the top costs $.20/square foot, determine the dimensions of the box that can be constructed at minimum cost
:
Let y = the cost of the box
:
Let x = one side of the square base
:
Let h = height of the box
:
We know that the box has to be 20 cu ft:
x^2*h = 20
h = (20/x^2)
:
Costs:
Base = .30(x^2)
Top = .20(x^2)
1 side = .10(x*(20/x^2)) = .10(20/x)
4 sides = .40(20/x) = 8/x
:
Total cost:
y = Base + Top + 4 sides
y =.30(x^2) + .20(x^2) + 8/x
y = .5x^2 + 8/x
Graph it:
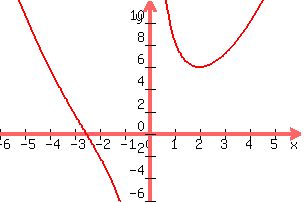
:
Looks like min cost (y) occurs when x = 2 ft, looks like a cost(y) of $6.00
:
Then the height = 20/2^2 = 5 ft
:
What is the cost then?
top .30(2^2) = 1.20
bot .20(2^2) = 0.80
hth .10(2*5) = 1.00 * 4 sides = $4.00
Total cost = $6.00 like the graph indicates.
:
Check: 2 * 2 * 5 = 20 cu ft as required
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|