SOLUTION: What is a cubic polynomial function in standard form with zeros 4, 2, and 4?

Click here to see ALL problems on Complex Numbers

Question 613334: What is a cubic polynomial function in standard form with zeros 4, 2, and 4?
Found 3 solutions by ewatrrr, htmentor, solver91311:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!

Hi,
(x-4)(x-2)(x-4) = 0
(x^2 - 6x + 8)(x-4) = 0
x^3 -6x^3 + 8x - 4x^3 + 24x -32 = 0
f(x) = x^3 - 10x^2 + 32x - 32

Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website!
What is a cubic polynomial function in standard form with zeros 4, 2, and 4?
=====================
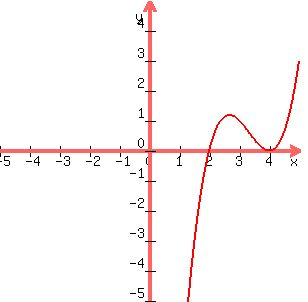
Zeros at 4, 4 and 2 means the function can be factored as:
(x-2)(x-4)^2 = 0
Multiply and collect terms
(x-2)(x^2 - 8x + 16) -> x^3 - 8x^2 + 16x - 2x^2 + 16x - 32 -> x^3 - 10x^2 + 32x - 32
So the function in standard form is
x^3 - 10x^2 + 32x - 32
The graph is below:

Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!

If it has zeros of 4, 4, and 2, then it has factors of (x - 4)(x - 4)(x - 2)

so

Multiply it out and collect like terms

John

My calculator said it, I believe it, that settles it