Question 612760: a square of 400 cm squared has the same perimeter as a rectangle whose length is 8 cm more than its length. find the area of the rectangle.
Answer by radh(108)   (Show Source):
You can put this solution on YOUR website! We know that to get the area of a square, we use  . In this case, we know the area, not the side. We have to find the side by plugging in what we know and isolating the variable.  . So, to find s, we take the square root of 400 which is 20. Now we know that each side of the square is 20 cm. To find perimeter, you just multiply a side by 4 (in the case of a square).  . The perimeter is 80 centimeters.
We know that the length is the same as the square's, plus 8. 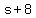 . Let's plug in what we know from before:  . So, the length of the rectangle is 28. What is the width? We know that the perimeter of the rectangle is the same as the square. To find the perimeter of a rectangle, the formula is  . Let's plug in what we know: 
Simplify:  to  to 
Now we know that the width is 12 and the length is 28. To find the area, you use this formula:  . Let's plug in what we know 
So, the area of the rectangle is 336 cm.
|
|
|
