SOLUTION: write a rule for the nth term of the arithmetic sequence 1. a11=29; a20=101 2.a6=-31; a14=-135

Algebra ->  Sequences-and-series -> SOLUTION: write a rule for the nth term of the arithmetic sequence 1. a11=29; a20=101 2.a6=-31; a14=-135      Log On


   

Question 612425: write a rule for the nth term of the arithmetic sequence
1. a11=29; a20=101
2.a6=-31; a14=-135
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The formula to learn for the nth term of arithmetic
sequences is:

an = a1 + (n-1)·d
I'll work the second one.  But I'll just give you the answer 
to the first one, so you'll have to do it by yourself, but 
you do it exactly like the second one. 

The answer to the first one is

an = 8n - 59 

---------------------

2. a6=-31; a14=-135

an = a1 + (n-1)·d


Substitute n=6

a6 = a1 + (6-1)d
-31 = a1 + 5d

Substitute n=14

a14 = a1 + (14-1)d
-135 = a1 + (13)d
-135 = a1 + 13d


So we have the system of equations:

-135 = a1 + 13d
 -31 = a1 +  5d
Multiply the second equation through by -1

-135 =  a1 + 13d
  31 = -a1 -  5d

Add those two equations:

-135 =  a1 + 13d
  31 = -a1 -  5d
-----------------

-104 =       8d

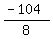%28-104%29%2F8 = d
-13 = d


Substituting that in

 -31 = a1 + 5d
 -31 = a1 + 5(-13)
 -31 = a1 - 65
  34 = a1 

So 

an = a1 + (n-1)·d

becomes

an = 34 + (n-1)·(-13)

an = 34 - 13(n-1)

an = 34 - 13n + 13

an = 47 - 13n

Edwin