You can
put this solution on YOUR website! In how many years will an account double itself at 5% interest compounded annually
Use the formula
A = P(1 +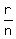 
)nt
Where
A = the final amount
P = the beginning amount
r = the annual rate expressed as a decimal
n = the number of times per year interest is compunded
t = the number of years invested
In the case the interest is compounded 1 time per year,
so the n's are just 1 and we can write the formula as
A = P(1 + r)t
We want to find t when the final amount A is twice the beginning
amount P. So we substitute 2P for A, and .05 for r
2P = P(1 + .05)t
2P = P(1.05)t
We divide both sides by P and get
2 = (1.05)t
We lake logs of both sides:
log(2) = log(1.05)t
Then we use a rule of logarithms which allows us to
write the exponent t as a coefficient of the log:
log(2) = t·log(1.05}
We divide both sides by log(1.05)
= t
Use a calculator to get the left side:
14.20669908 = t
It will not quite be doubled after 14 years, but it will be
more than doubled after 15 years.
Edwin
