|
Question 611140: Solve for X and just the real numbers
2X^3-5X^2+6X-2=o
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, with an exponent of 3, this is not a quadratic equation. So I have reset the category to the appropriate one. Choosing the right category for your problems will increase your chances of a quick reply from a tutor.

To solve an equation like this we first want a zero on e one side. We have that already so we can go to step 2: Factor. This polynomial- does not have a greatest common factor (other than 1).
- has too many terms for factoring by patterns (which all have 2 or three terms)
- has too many terms for trinomial (three terms) factoring
All that is left if factoring by grouping and factoring by trial and error of the possible rational roots. While it may be possible to factor this by grouping, I do not see it. Factoring by trial and error, as the name might suggest, can be tedious because of the "error" attempts that are often involved. Most use it as a factoring method of last resort. But that is where we are. This is the only factoring method we have left to try.
The possible rational roots of a polynomial are all the ratios, positive and negative, that can be formed using a factor of the constant term on top over a factor of the leading coefficient on the bottom. For your polynomial the constant term is the -2 at the end. Its factors are 1 and 2. Your leading coefficient is the 2 in front of the  . Its factors are also 1 and 2. This makes the possible rational roots: . Its factors are also 1 and 2. This makes the possible rational roots:
1/1 or 1, -1/1 or -1, 2/1 or 2, -2/1 or -2, 1/2 or -1/2
Now we try out these possible roots looking for an actual root (i.e. an x value that makes the polynomial equal to zero). There are some shortcuts that can sometimes help you narrow down your search. Your polynomial, with its alternating signs (+ then - then + then -), will not have any negative roots. (See if you can figure out why. Try some negative number for x and see of things work out.) So we can immediately rule out half of the possible rational roots. Now we're down to
1, 2, 1/2
Trying 1 as a possible root is easy because of how easy it is to raise 1 to various powers. Most people can do this in their head. With your polynomial we get: 2-5+6-2 = 1. Since we did not get zero, 1 is not a root.
You might try 2 mentally but it is not easy. Instead I will use synthetic division. (I hope you have learned synthetic division.) Trying 2:
2 2 -5 6 -2
4 -2 8
----------------
2 -1 4 6
The number in the lower right corner, the 6, is the remainder. The remainder also turns out to be the value of the polynomial when x = 2 so 2 is not a root either. Last of all we try 1/2:
1/2 2 -5 6 -2
1 -2 2
----------------
2 -4 4 0
Bingo! We have a zero as a remainder so x = 1/2 is a root of your polynomial. This means that 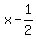 is a factor of your polynomial. (See if you can figure out why.) And not only have we found a root and a factor, the rest of the bottom row tells us the other factor. The "2 -4 4" translates into is a factor of your polynomial. (See if you can figure out why.) And not only have we found a root and a factor, the rest of the bottom row tells us the other factor. The "2 -4 4" translates into 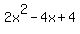 . So . So

in factored form is

Even though we have run out of rational roots, we are not finished looking for roots. There are three roots for a polynomial with a high exponent of 3. Fortunately the "other" factor we have is a quadratic. So we can use the Quadratic Formula on 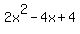 to find the irrational or complex roots that remain: to find the irrational or complex roots that remain:

Simplifying:


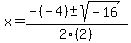
With the negative number in the square root, we can tell that the two roots we are about to find will be complex roots, not real roots. Since the problem asks only for real roots we can stop here. Your polynomial has only one real root: 1/2. The other two roots are complex.
In case you are curious, I'm going find the complex roots anyway. Continuing to simplify:





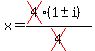

The three roots to your polynomial are 1/2 (real), 1 + i (complex) and 1 - i (complex).
|
|
|
| |