Question 611138: find all solutions in the interval [0,2pi): 2sin^2x-5sinx=-3
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Solving Trig equation often involve three stages:- Use algebra and/or Trig properties to transform the given equation into one or more equations of the form:
TrigFunction(expression) = number - Since Trig functions are periodic, the equation(s) from stage 1 will usually have an infinite number of solutions. Find the general solution (which expresses these infinite solutions) to the equation(s) from stage 1. (More on this when we get there.)
- Use the general solution(s) from stage 2 to find specific solutions if they are requested. Many problems, like this one, specify that only certain solutions are to be found, like "the smallest positive solution" or "all solutions within a given interval".
Let's see this in action:
1. Transform the equation...
Since  has only sin(x) in it, it is reasonable to assume that the equations we are looking for will be in the form: has only sin(x) in it, it is reasonable to assume that the equations we are looking for will be in the form:
sin(x) = number
And it might be easier to see how to do this if we use a temporary variable:
Let q = sin(x).
Replacing sin(x) with q our equation becomes:

Looking at the equation this way we can see that it is quadratic. So we want one side to be zero. Adding 3 we get:

Now we factor:
(2q-3)(q-1) = 0
From the Zero Product Property we know that one of these factors must be zero. So
2q - 3 = 0 or q - 1 = 0
Solving these we get:
q = 3/2 or q = 1
We can now replace the q's with sin(x) to get:
sin(x) = 3/2 or sin(x) = 1
If we know sin well, we know that it can never be 3/2. So that equation is impossible and we will reject it. Now we have only one equation:
sin(x) = 1
This is in the desired form.
2. Find the general solution.
A sin value of 1 is a special angle value so we should know what angles have 1 for a sin: 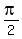 and any other angle that is co-terminal with and any other angle that is co-terminal with 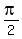 . The way we express this in an equation is: . The way we express this in an equation is:

Notes:- The "+
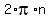 " is a way to express the idea of "and all co-terminal angles". " is a way to express the idea of "and all co-terminal angles". - The "n" in
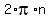 represents any and all integers. represents any and all integers. - As you replace the "n" with all the different integers (and don't forget the negative ones), you get different x values, all of which have a sin of 1. This "+
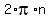 " is how we can express the infinity of solutions without having to list an infinity of numbers. " is how we can express the infinity of solutions without having to list an infinity of numbers.
3. Find specific solutions.
You problem requests solutions in the interval [0,  ). Now we just start replacing the "n" with different integers until we are satisfied that we have found all the x's that are in that interval. If we try n = 0 we get ). Now we just start replacing the "n" with different integers until we are satisfied that we have found all the x's that are in that interval. If we try n = 0 we get 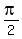 for x. This is in the interval. It should not take use too long to figure out that positive n's will lead to x's that are too large (i.e. larger than for x. This is in the interval. It should not take use too long to figure out that positive n's will lead to x's that are too large (i.e. larger than  and that negative n's will lead to x's that are too small (i.e. below 0), So there is only one x in the specified interval: x = pi/2. and that negative n's will lead to x's that are too small (i.e. below 0), So there is only one x in the specified interval: x = pi/2.
Final note: If you have not used temporary variables much, then they can be a little confusing. Just know that you, the problem solver, can always define a new variable in any way that you choose. In this problem, using the temporary variable helped us see how to proceed with the problem. After you get some practice with this, you will no longer need a temporary variable. You will learn to see that

is a quadratic equation. And you will see how

factors into

etc.
|
|
|