Question 611008: Factor completely Remember to look first for a common factor. Check by multiplying. If a polynomial is prime, state this.
2x^3 - 40x^2 + 192x
Found 3 solutions by richwmiller, lynnlo, ashipm01:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by ashipm01(26)   (Show Source): (Show Source):
You can put this solution on YOUR website! The common factor between all three terms is 2x, so you can factor that out first resulting in the following expression:
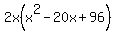
Now the second-degree polynomial can be factored normally by looking for two numbers that multiply together and result in 96 and add together to equal -20. The prime factors of 96 are 2, 2, 2, 2, 2, 3 so any distinct way to split those prime factors into two groups will yield a different pair of numbers that will multiply together to form 96. For example, the grouping {2, 2, 2} {2, 2, 3} will result in 8 * 12 (the product of each term in the prime factor group). But 8 + 12 = 20 and not -20, however if the numbers were -8 and -12 then they would add together to equal -20 and they would multiply together to equal 96.
So knowing the correct factors for the expression, it can now be rewritten as following:
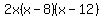
|
|
|