SOLUTION: I need help solving this problem The length of a rectangular pool is 4 ft longer than the width. The area of the swimming pool measures 60 square ft. Find the dimensions of the

Algebra ->  Rectangles -> SOLUTION: I need help solving this problem The length of a rectangular pool is 4 ft longer than the width. The area of the swimming pool measures 60 square ft. Find the dimensions of the       Log On


   

Question 610945: I need help solving this problem
The length of a rectangular pool is 4 ft longer than the width. The area of the swimming pool measures 60 square ft. Find the dimensions of the pool.
Answer by radh(108) About Me  (Show Source):
You can put this solution on YOUR website!
Let's write this word problem mathematically and remove excess. First of all, we know that l%2Aw=a.
The length of a rectangular pool is 4 ft longer than width (w+4). The area (*, not adding) measures 60 square feet.

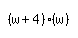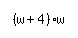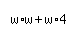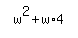To write this mathematically, it'd turn into: %28w%2B4%29%2A%28w%29=60. We can simplify that: simplify_cartoon%28+%28w%2B4%29%2A%28w%29+%29.

We'd then move the 60 to the other side to get: w%5E2%2B4w-60=0
Use the quadratic formula to get your solutions:

Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B4x%2B-60+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A1%2A-60=256.

Discriminant d=256 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-4%2B-sqrt%28+256+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%284%29%2Bsqrt%28+256+%29%29%2F2%5C1+=+6
x%5B2%5D+=+%28-%284%29-sqrt%28+256+%29%29%2F2%5C1+=+-10

Quadratic expression 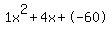1x%5E2%2B4x%2B-60 can be factored:
1x%5E2%2B4x%2B-60+=+%28x-6%29%2A%28x--10%29
Again, the answer is: 6, -10. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B4%2Ax%2B-60+%29

Because there can't be a negative in getting a positive area, we'd assume x is 6.

Let's go back into the normal equation to check the length and the width: %286%2B4%29%2A%286%29=60. It's correct, so we know that length is 10 and width is 6. :)