Question 61048: on a true/false test a student has no idea what the answers are to 3 of the questions so he guesses. What is the probability that he will guess correctly on all 3 questions? at least 2 times?
Answer by funmath(2933)   (Show Source):
You can put this solution on YOUR website! on a true/false test a student has no idea what the answers are to 3 of the questions so he guesses. What is the probability that he will guess correctly on all 3 questions? at least 2 times?
There's 1 write answer out of two choices for each question. Therefore there's a  probability of guessing all three questions right.
Percetagewise that's 12.5%. Note that that's the same probability of getting them all wrong (think about it.).
At least two right is 2 out of three and 3 out of three
There are three ways to get 2 right (wrr),(rwr),(wrr) and one way to get them all right (rrr)
 ++
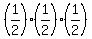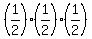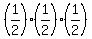
 ways to get 2 right
 ways to get 3 right
 ways to get 2 or 3 right. Note that this is the same probability of getting less than 2 right. (think about it.)
You can use binomial probability for this, but it would only be easier to do for a problem this small if you have a capable calculator. If you have a TI-83 or 84. Just hit, binomialpdf(3,.5,2)+binomialpdf(3,.5,3)=.5 or 1/2.
:
The formula for binomial probability is:
P(x)=probability of x
n=number of trials
x=number of successes
p=probabillty of success
q=1-p=probabilty of failure
For the probability of 2 correct answers:
n=3, x=2, p=1/2=.5, q=1-1/2=.5
For the probabilty of 3 correct answers:
n=3, x=3, p=.5, q=.5
Happy Calculating!!!
|
|
|
