|
Question 610466: Sandra and Pete are washing cars for a fundraiser. Working together, they can wash a car in 24 minutes. Sandra gets distracted by a call from her mother, so Pete starts washing a car on his own. After Pete has been working for 10 minutes, Sandra joins him and they work together for an additional 20 minutes. How long would it take Pete to wash a car alone?
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! Sandra and Pete are washing cars for a fundraiser. Working together, they can wash a car in 24 minutes. Sandra gets distracted by a call from her mother, so Pete starts washing a car on his own. After Pete has been working for 10 minutes, Sandra joins him and they work together for an additional 20 minutes. How long would it take Pete to wash a car alone?
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S washes alone washing 1 car
P washes alone washing 1 car
S and P washing 1 car together
P washing alone for 10 minutes
S and P washing together 20 min
We want to know how long it would take Pete to wash 1 car working alone, so we let that
answer be x. So we put 1 for the number of cars washed for "P washes alone
washing 1 car" and x for his number of minutes:
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S washes alone washing 1 car
P washes alone washing 1 car 1 x
S and P washing 1 car together
P washing alone for 10 minutes
S and P washing together 20 min
We also could have been asked how long it would take Sandra to wash 1 car
working alone, so we let that answer be y. So we put 1 for the number of cars
washed for "S washes alone washing 1 car" and y for her number of minutes:
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S washes alone washing 1 car 1 y
P washes alone washing 1 car 1 x
S and P washing 1 car together
P washing alone for 10 minutes
S and P washing together 20 min
Next we fill in their combined rate. We are told that working together they
can wash 1 car in 24 minutes so we fill in 1 for the number of cars and 24
for the number of minutes for "S and P washing 1 car together"
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S washes alone washing 1 car 1 y
If P washes alone washing 1 car 1 x
S and P washing 1 car together 1 24
P washing alone for 10 minutes
S and P washing together 20 min
Next we fill in their rates 1/y, 1/x, 1/24 in cars/minute by dividing
the number of cars, (1), by number of minutes, (y), (x), and 24
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S washes alone washing 1 car 1 y 1/y
P washes alone washing 1 car 1 x 1/x
S and P washing 1 car together 1 24 1/24
P washing alone for 10 minutes
S and P washing together 20 min
Also fill in the rate 1/x for "P working alone for 10 minutes" and 10 for
the number of minutes, and 1/24 for "S and P washing together for 20 min"
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S washes alone washing 1 car 1 y 1/y
P washes alone washing 1 car 1 x 1/x
S and P washing 1 car together 1 24 1/24
P washing alone for 10 minutes 10 1/x
S and P washing together 20 min 20 1/24
Next we fill in the fractions of a car washed in those two intervals
of time by multiplying the number of minutes by the rate:
Number of cars Number of Rate
washed or fraction minutes in
thereof worked cars/minute
S wasjes alone washing 1 car 1 y 1/y
P washes alone washing 1 car 1 x 1/x
S and P washing 1 car together 1 24 1/24
P washing alone for 10 minutes 10/y 10 1/x
S and P washing together 20 min 20/24 20 1/24
The two equations come from
 + +  = =  and
and
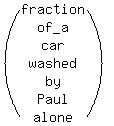 + +  = = 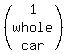 So we have this system of equations:
So we have this system of equations:
 Solve the second equation for y:
Solve the second equation for y:
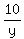 + + 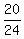 = 1
Reduce = 1
Reduce 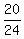 to to 
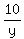 + +  = 1
Multiply thru by 6y
60 + 5y = 6y
60 = y, so it would take Sandra 60 minutes to wash 1 car.
Substitute in the first equation of the system: = 1
Multiply thru by 6y
60 + 5y = 6y
60 = y, so it would take Sandra 60 minutes to wash 1 car.
Substitute in the first equation of the system:

 Multiply through by 120x
2x + 120 = 5x
120 = 3x
40 = x
So it would take Pete 40 minutes to wash 1 car.
Edwin
Multiply through by 120x
2x + 120 = 5x
120 = 3x
40 = x
So it would take Pete 40 minutes to wash 1 car.
Edwin
|
|
|
| |