SOLUTION: I am having difficulty in solving this equation: sqrt(x/(1-x))+sqrt(1-x)-(5/2)=0

Algebra ->  Radicals -> SOLUTION: I am having difficulty in solving this equation: sqrt(x/(1-x))+sqrt(1-x)-(5/2)=0      Log On


   

Question 609879: I am having difficulty in solving this equation:
sqrt(x/(1-x))+sqrt(1-x)-(5/2)=0
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
sqrt%28x%2F%281-x%29%29%2Bsqrt%281-x%29-%285%2F2%29=0
I've spent a good deal of time on this problem and the only thing I have determined is that there must be a mistake. One (or more) of the following must be true:
  • I made a mistake while trying to solve the problem.
  • You made a mistake in what you posted.
  • The problem given to you has a mistake in it making it nearly insolvable.
I'm proceeding with a response in hopes that you can gain from what I've done and perhaps solve the problem correctly on your own.

First, I'm going to explain why the solutions, if any, have to be in the interval 0+%3C=+x+%3C+1:
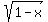  • From sqrt%281-x%29 we know that 1-x+%3E=+0 because the radicand (the number inside) of a square root can never be negative.
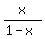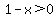  • But 1-x is also the denominator of x%2F%281-x%29 and denominators cannot be zero. So 1-x+%3E+0. Solving this we get x < 1.
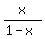  • The other radicand, x%2F%281-x%29, also cannot be negative. So x%2F%281-x%29+%3E+=+0. We have already found that 1-x must be positive. So for this fraction to be non-negative x must be zero or positive: x+%3E=+0
  • Putting this all together we find the 0+%3C=+x+%3C+1. Knowing this will save time later.
Next, I'm going to describe a general procedure for solving equations like this one:
  1. Isolate a square root.
  2. Square both sides of the equation. (Squaring the isolated square root should be easy. Be careful when squaring the other side of the equation.
  3. If there are still square roots in the equation, repeat steps 1-3.
  4. At this point there should be no square roots left. Use appropriate techniques to solve the equation you now have.
  5. Check your solution(s). This is not optional! Whenever you square both sides of an equation, like you've done at least once to get this far, extraneous solutions may be introduced. Extraneous solutions are solutions that fit the squared equation but do not fit the original equation. They can happen even if no mistakes have been made! So you must check your solutions in the original equation and reject any that do not work.
Last of all, I'm going to show you this procedure in action. Even though I end up not finding any solutions, following the procedure may teach some things that can help you with this and similar problems. (If you've correctly posted your problem, please check my work. Maybe you will find a mistake I've made and be able to find solutions!)

Before I start the procedure, I'm going to simplify the equation a little.
sqrt%28x%29%2Fsqrt%281-x%29%2Bsqrt%281-x%29-%285%2F2%29=0

sqrt%28x%29%2Bsqrt%281-x%29%2Asqrt%281-x%29-sqrt%281-x%29%285%2F2%29=0
sqrt%28x%29%2B1-x-%285%2F2%29sqrt%281-x%29=0
Now the procedure:
1. Isolate a square root.
Adding 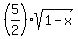%285%2F2%29sqrt%281-x%29%29 to each side:
sqrt%28x%29%2B1-x+=+%285%2F2%29sqrt%281-x%29
Note: Coefficients in front of the isolated square root, like the 5/2, are not a problem. If it really bothers you, you can multiply each side by 2/5 and get rid of it.

2. Square both sides.
%28sqrt%28x%29%2B1-x%29%5E2+=+%28%285%2F2%29sqrt%281-x%29%29%5E2
Squaring the right side is easy. The left side is a bit challenging:
%28sqrt%28x%29%2B1-x%29%2A%28sqrt%28x%29%2B1-x%29+=+%2825%2F4%29%281-x%29%29
On the left side we multiply each term of one factor by each term of the other:

Adding like terms (and re-ordering them) we get:
x%5E2+-x+%2B+2sqrt%28x%29+-2x%2Asqrt%28x%29+%2B+1+=+%2825%2F4%29-%2825%2F4%29x

3. If there's a square root, repeat. There is a square root so we repeat.

1. Isolate a square root.
First I'm going to get rid of the fractions by multiplying each side by 4:
4x%5E2+-4x+%2B+8sqrt%28x%29+-8x%2Asqrt%28x%29+%2B+4+=+25-25x
Next I'll gather the square root terms on the right side and the other terms on the left side:
4x%5E2+%2B21x+%2B+-21+=+8x%2Asqrt%28x%29+-8sqrt%28x%29
Factor out 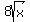8sqrt%28x%29 on the right side:
4x%5E2+%2B21x+%2B+-21+=+8sqrt%28x%29%28x-1%29
And divide each side by x - 1:
%284x%5E2+%2B21x+%2B+-21%29%2F%28x-1%29+=+8sqrt%28x%29

2. Square both sides.
%28%284x%5E2+%2B21x+%2B+-21%29%2F%28x-1%29%29%5E2+=+%288sqrt%28x%29%29%5E2
Again, squaring the right side is easy. And squaring the denominator on the right side is not hard. Squaring the numerator is another story altogether!?


3. We can see that the square roots are finally gone. So we can proceed to step 4.

4. Solve the equation.
First let's simplify.
Adding like terms in the numerator:
%2816x%5E4%2B168x%5E3%2B273x%5E2-882x%2B441%29%2F%28x%5E2-2x%2B1%29+=+64x
Multiply each side of the equation by 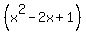%28x%5E2-2x%2B1%29:
16x%5E4%2B168x%5E3%2B273x%5E2-882x%2B441+=+%28x%5E2-2x%2B1%29%2A64x
16x%5E4%2B168x%5E3%2B273x%5E2-882x%2B441+=+64x%5E3-128x%5E2%2B64x
The only way to solve this is to get a zero on one side and then try to factor. Subtracting the entire right side from each side we get:
16x%5E4%2B104x%5E3%2B401x%5E2-946x%2B441+=+0
The only way to factor this is by trial and error of the different possible rational roots. The possible rational roots are all the possible ratios, positive and negative, of a factor of the constant term, 441, over a factor of the leading coefficient, 16. There are quite a few possible rational roots since there are many factors of both 441 and 16. But from our initial analysis, we know that the roots, if any, must be in the interval 0+%3C=+x+%3C+1. This cuts down the possible roots considerably. We are left with:
1/2, 1/4, 1/8, 1/16, 3/4, 3/8, 3/16, 7/8/, 7/16 and 9/16
The easiest way to test these roots is with synthetic division. First we'll try 1/2:
1/2   16    104    401    -946    441
              8     56   457/2
     ---------------------------------
      16    112    457
I stop here because the fraction will not get canceled out eventually and 1/2 is a root only if the last number on the bottom row, the remainder, is zero.

Now we'll try 1/4:
1/4   16    104    401    -946    441
              4     27     107   -839/4
     ---------------------------------
      16    108    428    -839    not zero

I tried the other possible rational roots and I could not find any that worked. As I mentioned earlier, this means there is a mistake in either the posted question or in what I've done so far. I encourage you to check for either kind of error. If you find the error, I hope that the above will help you find the solution.

If you find an error in my work, please use the "Thank you" process on algebra.com to tell me about it. Thanks!