Question 60981: This is a two part question. Can anyone help me set these up. I seem to have issues with these slopes. Thanks!
Using point P(2,9) and Q (-3,3)
Find distance between P and Q.
Find the equation of the line passing through P and Q.
Thanks again!
Answer by joyofmath(189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The distance between two points if found by computing the hypotenuse of a right triangle using the Pythagorean Theorem  . .
In the case of P and Q, the length of one side of the triangle is found by calculating the distance between X values and the length of another side is found by calculating the distance between the Y values.
So, the y values are 2 and -3 and their difference is  . .
The y values are 9 and 3. Their difference  . .
Use the Pythagorean Theorem to find the shortest distance between these points, the hypotenuse of the triangle with sides 5 and 6.
 . So, . So,  so so  which is approximately which is approximately 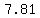 and that's the distance between the two points. and that's the distance between the two points.
The formula for a line is  where x is the slope and b is the y-axis intercept. The slope is the ratio of the change in x to the change in y. where x is the slope and b is the y-axis intercept. The slope is the ratio of the change in x to the change in y.
We know from our work above that the x increases by 6 for every increase in 5 that the y goes up.
So, the slope is:  . .
So, the equation of the line is:  . .
We need to find x.
We can use the x and y values of either point to do that.
Using Q, (-3,3) we find that  . .
Or, 
Or,  . .
So,  . .
Thus, the equation of the line is  . .
We verify this with both points:
If x = -3 and y = 3 then  so so  . .
If x = 2 and y = 9 then  so so  . .
|
|
|