Question 60968: find the units digit of 3^13*7^14 without actual multiplication
Answer by joyofmath(189)   (Show Source): (Show Source):
You can put this solution on YOUR website! We're looking at 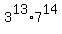
Well,  so so  ends in 3. ends in 3.
 ends in 3*3 or 9. ends in 3*3 or 9.
 ends in 9*3 =27 so it ends in 7. ends in 9*3 =27 so it ends in 7.
 ends in 7*3 = 21 so it ends in 1. ends in 7*3 = 21 so it ends in 1.
 ends in 1*3 or 3. So it ends in the same as ends in 1*3 or 3. So it ends in the same as  . .
 ends in 3*3 ends the same as ends in 3*3 ends the same as  . .
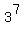 ends in 9*3 ends the same as ends in 9*3 ends the same as  . .
So, the pattern repeats every 4 powers. So,  ands with the same digit as ands with the same digit as 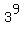 and and  which is 3. which is 3.
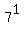 ends in 7. ends in 7.
 ends in the same digit as 7*7, or 9. ends in the same digit as 7*7, or 9.
 ends in the same digit as 9*7, or 3. ends in the same digit as 9*7, or 3.
 ends in the same digit as 3*7, or 1. ends in the same digit as 3*7, or 1.
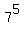 ends in the same digit as 1*7, which ends the same way as ends in the same digit as 1*7, which ends the same way as 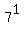 . .
So, this pattern also repeats every 4 powers.
So, 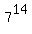 ends the same way as ends the same way as 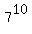 and and  and and  which is with a 9. which is with a 9.
So, 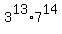 ends with the same digit as ends with the same digit as  which ends in 3 multiplied by the last digit of which ends in 3 multiplied by the last digit of 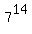 which is 9. which is 9.
So, the big product ends in  so 7 is the last digit of the big product. so 7 is the last digit of the big product.
|
|
|