Question 609502: Solve for x:
4(1+sin(x))=cos^2(x)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Solving equations like this usually involves three stages:- Use algebra and/or trig properties to transform the equation into one or more equations of the following form:
TrigFunction(expression) = number - Find the general equation for each of the equations from step 1. (Since the Trig functions are periodic there are an infinite number of solutions. The general solution will express this infinite set of solutions.)
- If the problem asks for one or more specific solutions (for example, "find the smallest positive solution" or "find all solutions in the interval
 ), then use the general solution to find the specific solution(s). ), then use the general solution to find the specific solution(s).
Let's see this in action:
1. Transform the equation into the desired form.
We'll start by simplifying the left side:

With two Trig functions in the equation, you will often want to use Trig properties to change one or both so that you only have one function in the equation. In this equation we should see that we can easily change the cos into sin using  : :

Since this is a quadratic equation so we want one side to be zero. Subtracting 1 and adding  (and rearranging the terms) we get: (and rearranging the terms) we get:

Now we can factor:
(sin(x) + 3)(sin(x) + 1) = 0
And from the Zero Product Property we get:
sin(x) + 3 = 0 or sin(x) + 1 = 0
Solving these we get:
sin(x) = -3 or sin(x) = -1
Since sin(x) cannot ever be -3, there are no solutions to the first equation. So we reject it and we're left with
sin(x) = -1
2. Find the general solution.
For a general solution to an equation of the form:
TrigFunction(expression) = number
we start by writing equations of the form:
expression = angle + 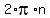
where "expression" is what the argument is for the function and "angle" is any angle which has the proper function value. You will need an equation for each different terminal side that has the proper function value. (Often you will need two equations. An example of this is provided after we finish this problem.) Repeat the above for each equation you got in step 1.
For your equation
sin(x) = -1
we will need only one equation in the general solution because we had only one equation from step 1 and because there is only one terminal side whose sin is -1. So the equation is:

NOTE 1: The 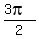 is there because its sin is -1. We could have any that terminates at the same place. For example we could have used is there because its sin is -1. We could have any that terminates at the same place. For example we could have used  instead. instead.
NOTE 2: The "+ 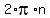 " is how we express the infinite set of angles that are solutions. It says, if effect, "and all co-terminal angles". " is how we express the infinite set of angles that are solutions. It says, if effect, "and all co-terminal angles".
NOTE 3: The "n" in 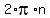 represents any and all integers. Some textbooks/teachers use a different letter, like "k". The letter used does not matter. What matters is that it represents any and all integers. represents any and all integers. Some textbooks/teachers use a different letter, like "k". The letter used does not matter. What matters is that it represents any and all integers.
Next, if "expression" (the left side of our equation(s)) is not just a variable, you would use algebra to solve for the variable. (Your equation has just "x" on the left side so we get to skip this step. The added axample at the end will show include step.)
3. Find the specific solution(s) if requested.
Your problem does not ask for a specific solution. So your solution is the general solution:

An example of a problem with multiple equations in the general solution, an "expression" that is not just a variable and with a specific solution:
Find all solutions to sin(2x) =  that are between 0 and that are between 0 and 
1. Transform the equation.
This equation is already in the
TrigFunction(expression) = number
form.
2. General solution
Here we will need two equations because there are two terminal sides (with a reference angle of  ) whose sin value is ) whose sin value is  , one in the 3rd and one in the 4th quadrant. For the 3rd quadrant we should get: , one in the 3rd and one in the 4th quadrant. For the 3rd quadrant we should get:

which simplifies to

For the 4th quadrant we can use

Next, since the left sides are not just "x", we need to solve for x. Dividing both sides by 2:


NOTE: Notice that we had to divide 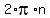 by 2 also! by 2 also!
3. Specific solution
Now we try different integers for "n" to find solutions in the desired interval. Keep trying different n's (and don't forget to try negative integers) until you're satisfied that you've found all the solutions. Looking at

we should be able to tell that 0 and all positive n's will give an x that is NOT between 0 and  . But is we use -1 for n we get . But is we use -1 for n we get 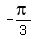 for x and this is between 0 and for x and this is between 0 and  . Other negative n's give us x's that are too small. Looking at . Other negative n's give us x's that are too small. Looking at

we should be able to tell that n = 0 gives us an x that is between 0 and  . Positive n's give us x's that are too big and negative n's give us x's that are too small. So the specific solutions to this problem are: . Positive n's give us x's that are too big and negative n's give us x's that are too small. So the specific solutions to this problem are:
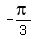 and and 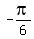 . .
NOTE: Do not expect that there will always be one specific solution from each equation of the general solution.
|
|
|