Question 609385: How do you solve sin(x/2)-cosx=0 with a restriction of [0,2pi)? We are supposed to be using the half angle formula...
Found 2 solutions by lwsshak3, Barbazzo:
Answer by lwsshak3(11628)   (Show Source):
You can put this solution on YOUR website! How do you solve sin(x/2)-cosx=0 with a restriction of [0,2pi)? We are supposed to be using the half angle formula
**
cos half-angle formula:
cos x/2=√[(1+cosx)/2]
√[(1+cosx)/2]-sinx=0
√[(1+cosx)/2]=sinx
square both sides
(1+cosx)/2=sin^2x=1-cos^2x
1+cosx=2-2cos^2x
2cos^2x+cosx-1=0
(2cosx-1)(cosx+1)=0
..
2cosx-1=0
cosx=1/2
x=π/3 and 5π/3
or
cosx+1=0
cosx=-1
x=π
Answer by Barbazzo(2) (Show Source):
You can put this solution on YOUR website! 
Transform Cos into Sin using Double Angle Identity: 
Let  , so 
Factor: 
Split into two equations:
 and 
For :
Take the inverse Sin:
 , where n is an integer
 , so no value of n is within the restriction 0 to 
not even n=0, since 
NOTE: x can't equal positive  since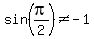 
and the given equation:  would not be true!
For :
Take the inverse Sin:
 , n must = 0, else not within restriction, so 
OR
 , n must = 0, else not within restriction, so 
So all values of x within restriction 0 to are:
( ,  )
|
|
|
