Question 609036: Find the exact value of the expression, cos^2(pi/8)-sin^2(pi/8)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 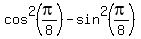
First of all, when you see/hear "exact value" in a Trig problem, you should know to put your calculator away. The problem can and must be solved using special angles.
But 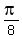 is NOT one of our special angles!? So how are we supposed to figure this out? Well, somehow we have to find a way to change each is NOT one of our special angles!? So how are we supposed to figure this out? Well, somehow we have to find a way to change each 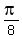 into one of the special angles. And there are a number of Trig properties/identities that allow you to change the argument of a trig function: into one of the special angles. And there are a number of Trig properties/identities that allow you to change the argument of a trig function:- Angle sum properties: sin(A+B), cos(A+B), tan(A+B)
- Angle difference properties: sin(A-B), cos(A-B), tan(A-B)
- The double angle properties: sin(2x), cos(2x) [of which there are 3 varieties), tan(2x)
- The half angle properties:
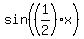 , , 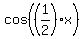 and and 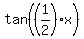
So which one(s) will help us change 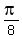 into a special angle. There are two clues: into a special angle. There are two clues:- If we notice that
 then a double angle property is suggested. then a double angle property is suggested. - Your expression fits the pattern of the right side of
 . .
NOTE: Trig will be a lot easier if you learn that these properties are patterns. The x's, A's and B's in all these properties are just placeholders. They can be replaced by any mathematical expression and the equation will still be true!! For example:




etc.
So we will use the cos(2x) property to rewrite
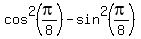
as
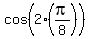
which simplifies as follows:
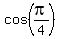

|
|
|