3x² + 7x = 12
So you asked if that becomes: x² +  x = 4?
No because the first step is to divide through by the
coefficient of x², which is 3. And we divide all the terms,
on both sides by 3
x = 4?
No because the first step is to divide through by the
coefficient of x², which is 3. And we divide all the terms,
on both sides by 3
 x² +
x² +  x =
x =  x² +
x² +  x = 4
So
x = 4
So  has the wrong enominator.
But it seems a shame to stop here and not go on and
complete the square. Let's do it just for fun:
(You can print it for future use, because you're
going to have to learn how to do that soon.
multiply
has the wrong enominator.
But it seems a shame to stop here and not go on and
complete the square. Let's do it just for fun:
(You can print it for future use, because you're
going to have to learn how to do that soon.
multiply  times
times  , get
, get  Square
Square  . get
. get 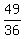 Add that to BOTH sides of the equation, to keep
it balanced.
So now we have:
x² +
Add that to BOTH sides of the equation, to keep
it balanced.
So now we have:
x² +  x+
x+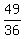 = 4+
= 4+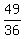 That factors as:
(x +
That factors as:
(x +  )² =
)² = 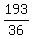 Now we use the principle of square roots:
x +
Now we use the principle of square roots:
x +  =
= 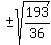 x +
x +  =
= 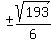 x =
x = 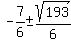 x =
x = 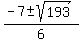 Edwin
Edwin