Question 608459: if sinx+sin^2x=1 ;then the value of cos^12x+3cos^10+3cos^8x+cos^6x+2cos^4x+2cos^2x-2
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! As posted, this is a very difficult problem. So either you are in an advanced class or you made a mistake in your posting.
A summary of the following solution:- Solve the equation for sin(x), (not x, sin(x)) [NOTE: sin(x) does not turn out to be a simple number (like 0, -1/2, 0, etc. This makes all the the remaining steps more difficult. If there is an error in your post it is probably in the equation. If so, then I hope the solution below will guide you through the solution with the correct equation.]
- Find
 using the answer from step 1. using the answer from step 1. - Use the answer from step 2 and
 to find to find  - Rewrite the cos expression in terms of
 [In the expression of cos's, all the cos's are raised to even powers and all even powers of cos can be expressed as powers of [In the expression of cos's, all the cos's are raised to even powers and all even powers of cos can be expressed as powers of  : :
( , ( , ( , ( , ( , etc.)] , etc.)] - Substitute the value from step 3 into the expression from step 4 and evaluate or use the Reminder Theorem to evaluate the expression from step 5. [Since sin(x) (and therefore
 and and  are not simple numbers, the Remainder Theorem will be easier (not easy, just easier) than substitution.] are not simple numbers, the Remainder Theorem will be easier (not easy, just easier) than substitution.]
1. Solve for sin(x):

Subtracting 1 from each side (and rearranging the terms):

An easier equation (perhaps the correct one) would factor at this point. This equation does not factor so we must use the Quadratic Formula:

Simplifying:




In other "words":
 or or 
Since the second equation gives us a sin(x) that is below -1, it is invalid and we must reject it. So:

2. Find 


You can use FOIL or the  pattern. Personally I like using the pattern: pattern. Personally I like using the pattern:

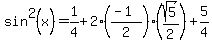

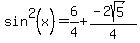

3. Find 


[Note the use of parentheses. Whenever you make substitutions, especially when you are substituting an expression of multiple terms, it is an extremely good habit to use parentheses!! In this case it helps us see that the square root term must be subtracted, too, not just the 3/2.]



4. Rewrite the cos expression in terms of powers of  : :

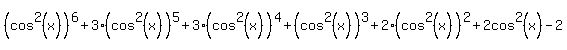
5. Use the value of  to evaluate the cos expression. [NOTE: If decimal approximations are OK, then I suggest you find the decimal approximation of to evaluate the cos expression. [NOTE: If decimal approximations are OK, then I suggest you find the decimal approximation of  and use that from this point on.] Often (and particularly with this problem) it is easier to use the Remainder Theorem to evaluate an expression like this. In short the Remainder theorem says that for some function f(x), f(a) will be the remainder of f(x)/(x-a). If you are unfamiliar or uncomfortable with this theorem or with synthetic division, then you will have to find all these powers of and use that from this point on.] Often (and particularly with this problem) it is easier to use the Remainder Theorem to evaluate an expression like this. In short the Remainder theorem says that for some function f(x), f(a) will be the remainder of f(x)/(x-a). If you are unfamiliar or uncomfortable with this theorem or with synthetic division, then you will have to find all these powers of  manually, substitute them in and simplify. Using synthetic division to find the remainder of dividing manually, substitute them in and simplify. Using synthetic division to find the remainder of dividing 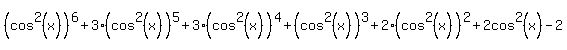 by by 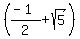 : :
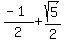 1 3 3 1 2 2 -2 1 3 3 1 2 2 -2
------------ 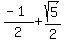  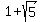 etc. etc.
-------------------------------------------
1 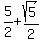 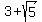 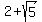 etc. etc.
I'll leave it up to you to finish. The number you end up in the lower right hand corner is the remainder (and the value of the expression).
|
|
|