I'll do it the algebra way, and then I'll do it the trigonometric way.
The ALGEBRA way:
4·sqrt(3+4i) = A + Bi, where A and B are real.
16(3 + 4i) = A² + 2ABi + B²i²
48 + 64i = A² + B²i² + 2ABi
48 + 64i = A² + B²(-1) + 2ABi
48 + 64i = A² - B² + 2ABi
48 = A² - B²
64 = 2AB
Solve the second equation for B: B = 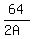 =
= 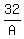 Substitute in 48 = A² - B²
48 = A² - (
Substitute in 48 = A² - B²
48 = A² - (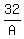 )²
48 = A² -
)²
48 = A² -  )
48A² = A4 - 1024
0 = A4 - 48A - 1024
0 = (A² - 64)(A² + 16}}}
A² - 64 = 0; A² + 16 = 0
A² = 64 A² = -16
A = ±8 A = ±4i (discard since A is real)
Using A = -8, = B =
)
48A² = A4 - 1024
0 = A4 - 48A - 1024
0 = (A² - 64)(A² + 16}}}
A² - 64 = 0; A² + 16 = 0
A² = 64 A² = -16
A = ±8 A = ±4i (discard since A is real)
Using A = -8, = B = 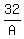 =
=  = -4
So one solution is A + Bi = -8 - 4i
Using A = 8, = B =
= -4
So one solution is A + Bi = -8 - 4i
Using A = 8, = B = 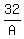 =
= 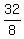 = 4
So the other solution is A + Bi = 8 + 4i
-------------------
The trigonometric way:
______
±4√3 + 4i
______
We'll just get ±√3 + 4i and multiply by 4 when we finish:
Get 3 + 4i in trigonometric form:
_______ ______ __
r = V3² + 4² = V9 + 16 = V25 = 5
θ = arctan(
= 4
So the other solution is A + Bi = 8 + 4i
-------------------
The trigonometric way:
______
±4√3 + 4i
______
We'll just get ±√3 + 4i and multiply by 4 when we finish:
Get 3 + 4i in trigonometric form:
_______ ______ __
r = V3² + 4² = V9 + 16 = V25 = 5
θ = arctan( = 53.13° + k·360°
Trig form is r(cos(θ+k*"350°") + isin(θ+k*"360°")),
3 + 4i = 5(cos(53.13°+k·360°) + i·sin(53.13°+k·360))
= 53.13° + k·360°
Trig form is r(cos(θ+k*"350°") + isin(θ+k*"360°")),
3 + 4i = 5(cos(53.13°+k·360°) + i·sin(53.13°+k·360))
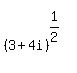 =
= 
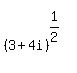 =
= 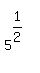
 =
=
 =
=
 , where k = 0, 1.
Answer is 4 times that or:
, where k = 0, 1.
Answer is 4 times that or:
 , where k = 0, 1.
That works out to be:
When k = 0
, where k = 0, 1.
That works out to be:
When k = 0
 ,
4(2.000000893 + .999992136i) or
8.000003573+3.999992854i
which is very close to 8+4i. The difference is because we
rounded off the angle.
When k = 1
,
4(2.000000893 + .999992136i) or
8.000003573+3.999992854i
which is very close to 8+4i. The difference is because we
rounded off the angle.
When k = 1
 ,
4(-2.000000893 - .999992136i) or
-8.000003573-3.999992854i
which is very close to -8-4i.
Edwin
,
4(-2.000000893 - .999992136i) or
-8.000003573-3.999992854i
which is very close to -8-4i.
Edwin