Question 607492: I believe you solve this word problem with Pythagorean Theorem..
A rectangle has a diagonal that measures 10 centimeters and a length that is 2 centimeters longer than the width. What is the width of the rectangle in centimeter?
I'd really appreciate some help!(:
Found 2 solutions by nerdybill, jsmallt9:
Answer by nerdybill(7384)   (Show Source):
You can put this solution on YOUR website! A rectangle has a diagonal that measures 10 centimeters and a length that is 2 centimeters longer than the width. What is the width of the rectangle in centimeter?
.
Let w = width
then
w+2 = length
.
applying Pythagorean theorem:
w^2 + (w+2)^2 = 10^2
w^2 + (w+2)(w+2) = 100
w^2 + w^2+4w+4 = 100
2w^2+4w+4 = 100
2w^2+4w-96 = 0
2w^2+16w-12w-96 = 0
(2w^2+16w)-(12w+96) = 0
2w(w+8)-12(w+8) = 0
(w+8)(2w-12) = 0
w = {-8, 12/2}
w = {-8, 6}
Throw out the negative solution (extraneous) leaving:
w = 6 cm
Answer by jsmallt9(3758)  (Show Source):
You can put this solution on YOUR website! Yes, the Pythagorean Theorem is correct for this problem.
The diagonal represents the hypotenuse of a right triangle and the length and width of the rectangle represent the legs. All we need to do is write expressions for the legs and we would be ready to use the Theorem:
Let x = the width of the rectangle. Then, since the length is two centimeters longer, x+2 represents the length.
In the Pythagorean Theorem equation,  , it is critical to know that the "c" must be the hypotenuse. (It doesn't matter which leg is "a" and which one is "b".) So our equation should be:
Now we solve for x. First we simplify. Be careful.  IS NOT 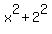 !!! You must use FOIL on (x+2)(x+2) or use the  pattern. I prefer using the pattern myself:
Next, since this is a quadratic equation, we want one side to be zero. Subtracting 100 from each side we get:
Now we factor (or use the Quadratic Formula). First, the GCF:
Next we factor the trinomial. The factors of -48 that add up to 2 are 8 and -6:
From the Zero Product Property we know that one (or more) of these factors must be zero. The 2 cannot be zero but the other factors could. So:
x + 8 = 0 or x - 6 = 0
Solving these we get:
x = -8 or x = 6
Since x represents the width of a rectangle and since we do not have negative sides on a rectangle, we reject the x = -8 solution. So the only possible width is 6. And, since the length is x+2, the length is 6+2 or 8.
|
|
|
