SOLUTION: Can someone please help me with this problem? If csc(x)=6, for 90degrees < x < 180degrees then, sin(pi/2)= cos(pi/2)= tan(pi/2)= Thank you!

Algebra ->  Trigonometry-basics -> SOLUTION: Can someone please help me with this problem? If csc(x)=6, for 90degrees < x < 180degrees then, sin(pi/2)= cos(pi/2)= tan(pi/2)= Thank you!      Log On


   

Question 607039: Can someone please help me with this problem?
If csc(x)=6, for 90degrees < x < 180degrees then,
sin(pi/2)=
cos(pi/2)=
tan(pi/2)=
Thank you!
Found 2 solutions by KMST, Gogonati:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You must have mixed part of a question with something else.
Or else this is a trick question.
pi%2F2 is 180%5Eo in degrees, and
sin%28pi%2F2%29=0 , cos%28pi%2F2%29=-1 , and tan%28pi%2F2%29=0 ,
regardless of the value 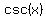x, or csc%28x%29 .

On the other hand, csc%28x%29=1%2Fsin%28x%29 , so
if csc%28x%29=1%2Fsin%28x%29=6 , then sin%28x%29=1%2F6
and since %28sin%28x%29%29%5E2%2B%28cos%28x%29%29%5E2=1, then
%28cos%28x%29%29%5E2=1-%281%2F6%29%5E2=1-1%2F36=35%2F36
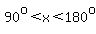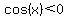
And if we also know that 90%5Eo%3Cx%3C180%5Eo, we know that cos%28x%29%3C0
so that would mean cos%28x%29=-sqrt%2835%2F36%29=-sqrt%2835%29%2Fsqrt%2836%29=-sqrt%2835%29%2F6
Then as tan%28x%29=sin%28x%29%2Fcos%28x%29 , we would have

Answer by Gogonati(855) About Me  (Show Source):
You can put this solution on YOUR website!
If cscx=6 then six=1/6; sin(pi/2)=1;cos(pi/2)=0 and tan(pi/2) doesn't exist.
If sinx=1/6 then x=sin^-1(1/6)=0.2618 radian.