Hi,
Ellipse:
where Pt(h,k) is the center.
a and b are the respective vertices distances from center and ±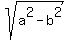
are the foci distances from center
Foci: (0,-3) and (0,3) 
,and major axis of 10 is along x = 0
3 =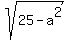 
, a = 4 |Note: (Distance from Center along major axis)^2 = 25
See below descriptions of various conics
Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is where Pt(h,k) is the center.
a and b are the respective vertices distances from center and ±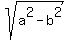are the foci distances from center
Standard Form of an Equation of an Hyperbola opening right and left is:
where Pt(h,k) is a center with vertices 'a' units right and left of center.
Standard Form of an Equation of an Hyperbola opening up and down is:
where Pt(h,k) is a center with vertices 'b' units up and down from center.
the vertex form of a parabola opening up or down, 
where(h,k) is the vertex.
The standard form is 
, where the focus is (h,k + p)
the vertex form of a parabola opening right or left, 
where(h,k) is the vertex.
The standard form is 
, where the focus is (h +p,k )
