Question 604675: Hi, I would like some help solving this equations:
a) x/6-3=-1
I tried
x/6-3=-1
+3=+3
x/6/2 = 2/2
x=12
b) 8x-5>13+2x
+5 +5
8x/8 18+2x/8x
x= 2.5
However don't think they are right.I appreciate your help.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the first problem, you are asked to solve:
.

.
The general plan will be to get the numbers on the right side of the equal sign and combine them, and get just x by itself on the left side.
.
So first, let's get rid of the -3 on the left side. We do this by adding +3 to the left side. But if we add +3 to the left side, we must also add +3 to the right side to keep the equation in balance. Adding +3 to both sides results in:
.

.
On the left side the -3 and the +3 cancel each other because they total zero. And on the right side the -1 and the +3 add to give +2. So by adding +3 to both sides the equation becomes:
.

.
Finally, to get rid of the 6 in the denominator of the left side, we multiply the left side by 6. When we do that, we must also multiply the right side by 6 to keep the equation in balance. So first let's do the multiplication of both sides by 6 as shown below:
.

.
On the left side the 6 in the numerator cancels with the 6 in the denominator as shown and on the right side the 6 times the 2 results in 12:
.

.
And we are left with the answer:
.

.
You had the correct answer, but I'm not exactly sure how you went about solving it. And since you were unsure of the answer, I expect that you were also unsure of what you did. It looks as if you correctly added the +3 to both sides, but you then appear to have divided both sides by 2 and that would not be a correct thing to do. The above explanation should help you see what you can do and why you do it.
.
Next you were given:
.
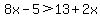
.
The plan for this is to work it as you would an equation, but instead of an equal sign you have an inequality sign. In general you can use the same procedures as you would for an equation, except that if you multiply or divide both sides by a negative number, you also reverse the direction of the inequality sign.
.
It appears as if you decided to add +5 to both sides of this inequality sign. That was correct. So let's do it here also:
.
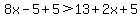
.
On the left side of the inequality sign the -5 and the +5 cancel each other. And on the right side the 13 and the +5 add together to give 18. The result is that when we add +5 to both sides we get:
.
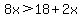
.
It now appears as if you decided to divide one side by 8 and the other side by 8x. This is not quite correct. The thing to do next is remember that we are trying to get all the numbers together on the right side and all the x terms combined on the left side. So let's get rid of the 2x on the right side by subtracting 2x from both sides. When we do that the inequality becomes:
.
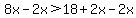
.
On the left side the 8x and the -2x combine to give 6x. And on the right side the +2x and the -2x cancel each other. So we are left with:
.

.
Finally, we can get rid of the 6 on the left side by dividing both sides of this inequality by +6 as shown below:
.
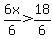
.
The six in the numerator of the left side cancels with the 6 in the denominator. And on the right side the 6 in the denominator divides into the 18 to give 3. So dividing both sides by 6 results in:
.
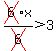
.
Which simplifies to:
.

.
This says that x is greater than 3. What this means is that the original inequality you were given will be true if x is a number greater than 3. Let's try it for a number greater than 3. Let's say that x is +4 and then let's substitute that value for x in the original inequality. The original inequality is:
.
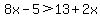
.
Substitute +4 for x and you have:
.
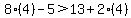
.
On the left side the 8 times 4 multiplies out to 32 and when you subtract 5 from that the left side reduces to 27. On the right side the 2 times 4 multiplies out to 8 and when you add that to 13 you get 21. So with x equal to +4 the original inequality becomes:
.

.
and this says that with x equal to 4 (which is greater than 3) the inequality tells us that 27 is greater than 21. This is correct and it gives us some assurance that if x is greater than 3, the inequality is likely correct.
.
Let's try the same sort of analysis using a value for x less than 3. Zero is less than 3 and it is easy to work with in this case. So let's set x equal to zero in the original inequality. When we substitute zero for x in the original inequality it becomes:
.
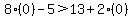
.
The two terms that are products involving zero disappear and the inequality simplifies to:
.

.
But this is not true. -5 is not greater than 13. So for one value of x that is less than 3 we know the inequality does not hold. This also helps us to say that x must be greater than 3 in order for the inequality to hold true.
.
So the answer to this second problem is that in order for the inequality to be true, x > 3 ... x must be greater than 3.
.
I hope that the above discussion of these two problems help you to understand how you can work through them to get a correct answer.
.
|
|
|