Question 60460: mama mia! for some reason, these sequences are just driving me mad! i would appreciate if you could help me with a few more problems. hopefully, something will click in my head after this.
Instructions: write the general term of the sequence:
#1. 1,2,3,4,5,6,...
(answer here) -> Nth term:____
i'm pretty sure the answer is just plain N, but i'm not sure.
#2. 1,2,4,8,16,...
(answer here) -> Nth term: ___
I know the answer involves the number 2 and N, but i'm not sure how to put them together correctly.
#10. 1,-1,1,-1,1,-1,...
Nth term:__
this one just left me clueless. i think it's -1n^0, but, i'm not sure.
#9. -1,4,-9,16,-25,...
Nth term:__
again, i think it's -n^3, but i'm not positive.
I'm also having trouble with adding terms in a sequence. i have a formula: [(first term + last term)(number of terms)]/2. but i'm not sure how i would apply it to sequences involving exponents.
Instructions: write the sum
#2. 1+3+9+27+81+...+1*3^101
Now, am i correct in assuming that 1*3 is the general term of the sequence and that the last term is the 101st value of 1*3?
#5 2+7+12+17+...+97
just plain lost on this one.
again, i thank you for your help in advance
Found 2 solutions by josmiceli, praseena:
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! I hope I can help. You'll do yourself (and your grades) a big favor
if you get in the habit of always checking your answers. Simply put,
that just means plugging your solution back into the original problem
and seeing if it's really true. Of course, you need to arrive at a solution
in the first place.
(1) 1,2,3,4,5,6
This has lots of names: counting sequence, cardinal numbers, etc.
Let's say 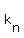 = the nth term, then = the nth term, then
 Remember what I said. Test it, even if it appears simple. Remember what I said. Test it, even if it appears simple.



looks OK
-------------
(2) 1,2,4,8,16
Don't rush to an answer. What do you see? Every term is even but the first
Ok, if they're even, they're divisible by 2. Write them differently
1
2
2*2
2*2*2
2*2*2*2
This is called a power sequence. You just have to write it with exponents.
n=1.....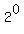
n=2.....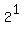
n=3.....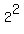
n=4.....
n=5.....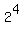 etc. etc.
Compare the exponent with it's position in the sequence. It looks like,
if the position is n, then the exponent is n-1, so if k is the general
term,
 As always, check the answer As always, check the answer


 ETC. ETC.
---------------------
#10. 1,-1,1,-1,1,-1,...
Again, k is the general term

check



These look OK. With practice you'll spot these things
--------------------
That's all I have time for. Hope it helps.
Answer by praseena(37)   (Show Source): (Show Source):
You can put this solution on YOUR website! first series is 1,2,3,4,5,6,7,..........
this is arithmatic series
here the first term is 1 and the common difference is i
now N th term of an arithmatic progression is given as a+(N-1)d, where a is the first term,N is the Nth term and d is the common difference.
so here the Nth term is 1 + ( N - 1 ) * 1 = 1 + N - 1 =
understood?
good
now next problem
The series is 1,2,4,8,6,........
this is also an arithmaticseries
here the first term is 1 and the common difference is 2
so the Nth term is given as,
1 + ( N - 1 ) * 2 = 1 + 2N -2
= 2N - 1
so for this series Nth term is 2N-1.
understood?
Next series is 1,-1,1,-1,1,-1,........
this series is a geometric series and here the first term is 1 and common ratio is -1
here the N th term is given by the formula,
An = a * r ^(n-1), where 'a' is the first term and 'r ' is the common ratio and ' n' represents nth term
so here the nth term is = 1 * ( -1 ) ^ (n-1)
here two possibilities are there,
one is , if n is an even number then ( n -1) is an odd number.
which means that (-1) ^( an odd number ) is always -1
if n is an odd number then (n-1) is an even number, which means (-1)^(an even number) is always an even number.
so we can conclude this answer like this,
if n is an even number, for the given series the nth term is -1
and if n is an odd number the nth term of the series is +1.
understood?
-1,4,-9,16,-25,...
here terms come like this
first term is -1, we can put it as -1*(1)^2
second term is 4, ==> - 1*(2)^2
third term is -9, that is, -1*(3)^2
and so on......
so we can write the nth term as, -1(n)^2
clear?
o.k.
next one is g
1+3+9+27+81+...+.........
first we have to identify the series.
here the terms are like this
first term is 1
second term is 3, which can be written as 1*3
third term is 9, ===> 1*3^2
fourth term is 27=1*3^3
and so on
so this is a geometric series.
the sum of nth term of a series given by the formula,
(Otherwise we can make out this from the above formation)
Sn = a * r ^ (n-1)
= 1 * 3 ^(n-1)
= 1 * 3 ^ (n-1).
clear?
o.k.?
now your doubt is,
1+3+9+27+81+...+1*3^101
am i correct in assuming that 1*3 is the general term of the sequence and that the last term is the 101st
here 1 * 3 ^101 MEANS this is the 100 th term of the series.
that means 1*3^(n-1) is the general term of the series.
o.k.?
next one is,
2+7+12+17+...+97
here the first term is 2
second term is 7= 2+5
third term is 12= 7+5
fourth term is 17=12+5
and so on......
thus the series forms by adding 5 to the previous term.
that is this one is an arithmatic series
here sum of first n terms of a series is given by the formulais,
n/2(first term +last term)
hwere the first term is 2 and the laqst term is 97so the sum of the seris is
n/2(2+97)
for calculating this sum, we need number of terms. right?
for that first of find out the number of terms in the series
we have the formula, a+(n-1)d for the nth term, here take 97 as the nth term
which comes like this,
a + ( n - 1 ) d = 97
2 + ( n -1) * 5 = 97
now subtract 2 from bopth sides of the equation
==> (n-1) * 5 = 95
divide by 5 on both sides
==> (n-1) = 95 / 5
==> n -1 = 19
add 1 on both sides of the equation
==> n =20
so the number of terms in the given series is 20. right?
so sum of the 20 terms of the given series is,
20 /2 (2 + 97 )
10 * 99 = 990
so the answer is 990.
|
|
|