Question 603245: I need help solving this non-linear equation using the elimination method...please help. x^2+3xy+y^2=27: x^2-xy+y^2=6 any help would be greatly appreciated
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Someone has probably solved similar problems and developed an easy general procedure that I've never heard of. Maybe it would help to realize that one of the equations represents an ellipse and the other a hyperbola, and to figure out their axes of symmetry
I'll just try something and see how it works.
If you were to subtract the second equation from the first one, you would have
 --> -->  --> -->  <---> <---> 
(That's the equation of a hyperbola that has the x-axis and the y-axis as asymptotes, and tells me that x and y are both positive or both negative).
If you multiply the second equation times 3 and add the first, you would have
 --> -->  --> -->  <---> <---> 
(That's the equation of a circle, centered at the origin,
with radius  ). ).
At this point I see two ways forward.
I can build expressions for  and and  , solve them for , solve them for  and and 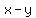 and end up with easy systems of linear equations: and end up with easy systems of linear equations:
 tells me tells me  or or 
 tells me tells me  or or 
That seems to give too many combinations, but from the 4 sytems of linear equations
 , ,  , ,  , and , and  , you easily get the answers: , you easily get the answers:
 , ,  , ,  , and , and  . .
Alternatively, I can work part of the previous option up to  or or 
and then use that along with 
to make two quadratic equations that will give me the answers.
We know that the quadratic equation  (z is the variable here), (z is the variable here),
with solutions  and and  , can also be written as , can also be written as

We make one of those quadratic equations with  , along with , along with  . .
We get  , which gives us two solutions for , which gives us two solutions for  . .
 , both positive. , both positive.
We can make  and and  or or
 and and  . .
With  and and  , we make , we make
 , which gives us two negative solutions , which gives us two negative solutions
 . .
We can make  and and  , or , or
 and and  . .
|
|
|