Question 602476: the length of the sides of a triangle are 6 inches, 8 inches, and 12 inches. Find the area of the triangle
Found 2 solutions by ewatrrr, jim_thompson5910:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Using Heron's Equation to find the area of a triangle when 3 sides are given
a = 6, b = 8 and c = 12 inches
 | s being the semi-perimeter = 26/2 = 13 | s being the semi-perimeter = 26/2 = 13
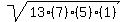 = 21.3307 square inches = 21.3307 square inches
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Hero's (or Heron's) Formula (Used to Find the Area of a Triangle Given its Three Sides) |
In order to find the area of a triangle 'A' with side lengths of 'a', 'b', and 'c', we can use Hero's Formula:
 where S is the semiperimeter and it is defined by where S is the semiperimeter and it is defined by 
Note: "semi" means half. So the semiperimeter is half the perimeter.
So let's first calculate the semiperimeter S:
 Start with the semiperimeter formula. Start with the semiperimeter formula.
 Plug in Plug in  , ,  , and , and  . .
 Add. Add.
 Divide. Divide.
----------------------------------------
 Now move onto Hero's Formula. Now move onto Hero's Formula.
 Plug in Plug in  , ,  , ,  , and , and  . .
 Subtract. Subtract.
 Multiply. Multiply.
 Take the square root of Take the square root of 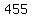 to get to get 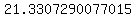 . .
So the area of the triangle with side lengths of  , ,  , and , and  is roughly is roughly 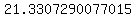 square units. square units.
|
|
|
|