|
Question 601695: Please help. I am confusing myself more every time I try to work this.
Factor the following expression completely:
12y5 34xy4 + 14x2y3
Also, if you could please tell me if I answered this right I would appreciate it.
Question: Andrew factored the expression 24x^3 8x^2 32x as 8x(3x^3 x^2 -4x) . But when Melissa applied the distributive law and multiplied out 8x(3x^3 x^2 4x), she got 24x^4 8x^3 32x; thus, Andrews solution does not appear to check. Why is that? Please help Andrew to understand this better. Explain your reasoning and correctly factor the original expression, if possible. If the expression is prime, so state.
Answer:Since Andrew stared his factoring with 8x he should have reduced the quotent inside the parenthesis by 1. Also Melissa should have gotten 24x^4 - 8x^3 - 34x^2. The correct answer should have been 8(3x^3 - x^2 = 4x) this would have checked to the beginning expression.
Thank you in advance!
Found 3 solutions by jim_thompson5910, Edwin McCravy, stanbon:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
 Start with the given expression. Start with the given expression.
 Factor out the GCF Factor out the GCF  . .
Now let's try to factor the inner expression 
---------------------------------------------------------------
Looking at the expression  , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is 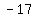 , and the last coefficient is , and the last coefficient is  . .
Now multiply the first coefficient  by the last coefficient by the last coefficient  to get to get  . .
Now the question is: what two whole numbers multiply to  (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient 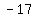 ? ?
To find these two numbers, we need to list all of the factors of  (the previous product). (the previous product).
Factors of  : :
1,2,3,6,7,14,21,42
-1,-2,-3,-6,-7,-14,-21,-42
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*42 = 42
2*21 = 42
3*14 = 42
6*7 = 42
(-1)*(-42) = 42
(-2)*(-21) = 42
(-3)*(-14) = 42
(-6)*(-7) = 42
Now let's add up each pair of factors to see if one pair adds to the middle coefficient 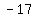 : :
| First Number | Second Number | Sum | | 1 | 42 | 1+42=43 | | 2 | 21 | 2+21=23 | | 3 | 14 | 3+14=17 | | 6 | 7 | 6+7=13 | | -1 | -42 | -1+(-42)=-43 | | -2 | -21 | -2+(-21)=-23 | | -3 | -14 | -3+(-14)=-17 | | -6 | -7 | -6+(-7)=-13 |
From the table, we can see that the two numbers  and and  add to add to 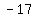 (the middle coefficient). (the middle coefficient).
So the two numbers  and and  both multiply to both multiply to  and add to and add to 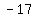
Now replace the middle term 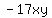 with with 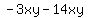 . Remember, . Remember,  and and  add to add to 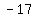 . So this shows us that . So this shows us that  . .
 Replace the second term Replace the second term 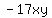 with with 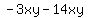 . .
 Group the terms into two pairs. Group the terms into two pairs.
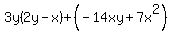 Factor out the GCF Factor out the GCF  from the first group. from the first group.
 Factor out Factor out  from the second group. from the second group.
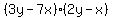 Factor out Factor out  from the entire expression. from the entire expression.
--------------------------------------------------------
So  factors to factors to 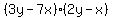
which means that  factors to factors to 
========================================================
Answer:
 completely factors to completely factors to 
===============================================================================
===============================================================================
# 2
Andrew forgot to factor out an x from each term as well. He should have gotten
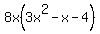
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Factor:
12y5 34xy4 + 14x2y3
Factor out 2y3
2y3(6y2 - 17xy + 7x2)
2y3(3y - 7x)(2x - y)
--------------------------------
Factor:
24x3 8x2 32x
8x(3x2 - x - 4)
8x(3x - 4)(x + 1)
Edwin
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help. I am confusing myself more every time I try to work this.
Factor the following expression completely:
12y5 34xy4 + 14x2y3
----
GCF: 2y^3
Factored form:
(2y^3)(6y^2 - 17xy + 7x^2)
===========================================
Also, if you could please tell me if I answered this right I would appreciate it.
Question: Andrew factored the expression
24x^3 8x^2 32x as 8x(3x^3 x^2 -4x) .
But when Melissa applied the distributive law and multiplied out 8x(3x^3 x^2 4x), she got 24x^4 8x^3 32x;
thus, Andrews solution does not appear to check. Why is that?
Andrew's answer should be: 8x(3x^2-x-4)
Please help Andrew to understand this better. Explain your reasoning and correctly factor the original expression, if possible. If the expression is prime, so state.
------------------------------
Answer:Since Andrew stared his factoring with 8x he should have reduced the quotent inside the parenthesis by 1. Also Melissa should have gotten 24x^4 - 8x^3 - 34x^2. The correct answer should have been 8(3x^3 - x^2 = 4x) this would have checked to the beginning expression.
------------------------------
True, but you still have a common factor of "x" in your answer.
The correct answer is 8x(3x^2-x-4)
======================================
Cheers,
Stan H.
=================
|
|
|
| |