Question 601505: The first snow blower can remove 20 cubic feet per minute, and the second blower can remove 60 cubic feet per minute.
Write and simplify an expression that gives the number of cubic feet of snow removed in x minutes.
Find the total number of cubic feet of snow removed in 36 minutes.
Which expression gives the number of cubic feet of snow removed in x minutes?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE FIFTH GRADER CALCULATIONS:
To find the amount of snow removed by one snow blower, you multiply the rate by the time the snow blower is working.
If the first snow blower works for 36 minutes at a rate of 20 cubic feet per minute, the amount of snow removed is
(20 cu.ft/minute)(36 minutes) = 720 cu.ft
In x minutes, it would remove
 cubic feet of snow. cubic feet of snow.
If the second snow blower works for 36 minutes at a rate of 60 cubic feet per minute, the amount of snow removed is
(60 cu.ft/minute)(36 minutes) = 2160 cu.ft
In x minutes, it would remove
 cubic feet of snow. cubic feet of snow.
With the two snow blowers working together, the amount removed in 36 minutes is
720 cu.ft + 2160 cu.ft = 2880 cu.ft
THE ALGEBRA POINT OF VIEW:
In algebra, we would write all the calculations in one step as
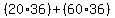 cubic feet, and we could make someone else calculate for us. cubic feet, and we could make someone else calculate for us.
Many centuries ago, people got sick and tired of writing that many parentheses, and decided to agree on rules for the ORDER OF OPERATIONS, saying that multiplications in between plus signs will be done first, before adding.
After that, the same calculation was written as
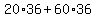
The same calculation can be done more efficiently as
 DISTRIBUTIVE PROPERTY DISTRIBUTIVE PROPERTY
we would multiply just once to calculate  . .
My explanations are surely wordy (and hopefully helpful, while entertaining), but I suspect the most that your teacher expects for the snow removed in 36 minutes is

ABOUT THAT DISTRIBUTIVE PROPERTY:
The concrete details of the case are different, but the abstract math part of the calculation is the same as the case of two pieces of 36-inch wide fabric, with lengths 20 and 60 inches.
 We can multiply twice to calculate the amount of fabric in each piece and then add to find the total: We can multiply twice to calculate the amount of fabric in each piece and then add to find the total:
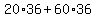 square inches of fabric square inches of fabric
or we could add the lengths, and then multiply the total length by the width of the fabric:
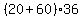
The result is the same: 
AND NOW WITH THAT x:
In x minutes one blower removes  cubic feet of snow, and the other removes cubic feet of snow, and the other removes 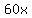 cubic feet of snow. cubic feet of snow.

applying the distributive property.
When we apply the distributive property that way, we often call the process "taking out a common factor."
So 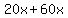 is the first written expression for the problem with x, is the first written expression for the problem with x,
and since  , ,
 is the simplified expression to calculate the cubic feet of snow removed in x minutes by two snow blowers with rates of 20 cubic feet per minute and 60 cubic feet per minute. is the simplified expression to calculate the cubic feet of snow removed in x minutes by two snow blowers with rates of 20 cubic feet per minute and 60 cubic feet per minute.
|
|
|