Question 601396: Form a polynomial whosezeros and degrees are given.
Zeros:-3,-2,3; degree 3
A)f(x)=x^3-2x^2-9x+18 for a= 1
B)f(x)=x^3+2x^2-9x-18 for a= 1
C)f(x)=x^3-2x^2+9x-18 for a= 1
D)f(x)=x^3+2x^2+9x+18 for a= 1
Found 2 solutions by Alan3354, w_parminder:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Form a polynomial whosezeros and degrees are given.
Zeros:-3,-2,3; degree 3
----------
Each zero, eg, z, contributes a factor (x - z)
Multiply (x+3)*(x-3)*(x+2)
---------------
= 
= 
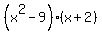
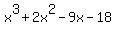
B
----
I don't know what the a= 1 means.
Answer by w_parminder(53)  (Show Source):
You can put this solution on YOUR website! Sorry dear, I can't understand the problem completely but I am solving it to form a polynomial whose zeros are -3, -2 & +3 with degree 3
The simple method to find the polynomial is just write the factors of it and multiply them.
In order to find the factors, just subtract the zeros separately from a variable say 'X'
So the factors of the polynomial are
X - (-3) i.e. (X + 3)
X - (-2) i.e. (X + 2) &
X - (+3) i.e. (X - 3)
on multiplying these factors, we will get the required polynomial,
i.e. (X + 3)(X + 2)(X - 3)
i.e.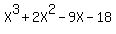 
Now I don't know what is A, B, C & D
If these are the options for the correct answer then what is 'a = 1'
Please reply
|
|
|
