SOLUTION: I have never been more confused in my life... I tried this for the first one but I don't think that I have it right PLease HELP!!!!! Thanks {{{fx=x^3-3x^2-2x+1}}} {{{fx=1^3-

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I have never been more confused in my life... I tried this for the first one but I don't think that I have it right PLease HELP!!!!! Thanks {{{fx=x^3-3x^2-2x+1}}} {{{fx=1^3-      Log On


   

Question 59961: I have never been more confused in my life... I tried this for the first one but I don't think that I have it right PLease HELP!!!!!
Thanks
fx=x%5E3-3x%5E2-2x%2B1
fx=1%5E3-3%281%29%5E2-2%281%29%2B1
fx=1-3-2+1
fx=3
I'm not too sure about this please please I really need help on this problem

Evaluate each of the functions below at x = 1, 2, 4, 8, and 16. Plot the graph of each function. Classify each as linear, quadratic, polynomial, exponential, or logarithmic, and explain the reasons for your classifications. Compare how quickly each function increases, based on the evaluations and graphs, and rank the functions from fastest to slowest growing.
- f(x) = x3 - 3x2 - 2x + 1
- f(x) = ex
- f(x) = 3x - 2
- f(x) = log x
- f(x) = x2 - 5x + 6
Answer by funmath(2933) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%29=x%5E3-3x%5E2-2x%2B1
f%281%29=1%5E3-3%281%29%5E2-2%281%29%2B1
f(1)=1-3-2+1
f(1)=3
:
You did this right. Do the same for each number. You'll need a scientific calulator for the exponential and logarithmic functions.
Evaluate each of the functions below at x = 1, 2, 4, 8, and 16. Plot the graph of each function. Classify each as linear, quadratic, polynomial, exponential, or logarithmic, and explain the reasons for your classifications. Compare how quickly each function increases, based on the evaluations and graphs, and rank the functions from fastest to slowest growing.
f%28x%29=x%5E3-3x%5E2-2x%2B1 This is a polynomial, because the degree is 3. Degree has to do with the highest exponent.
f(1)=3 Plot (1,3)
f%282%29=%282%29%5E3-3%282%29%5E2-2%282%29%2B1
f(2)=-7 Plot (2,7)
I'll leave the middle terms for you to calculate.
f(16)=3297
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2Cx%5E3-3x%5E2-2x%2B1%29
This is ranked second fastest.
:
f%28x%29=e%5Ex This is an exponential function, beacuse the variable is an exponent.
f%281%29=e%5E%281%29=2.7183 Plot (1,2.7)
f%282%29=e%5E2=7.3891 Plot(2,7.4)
f%2816%29=e%5E16=8886110.521
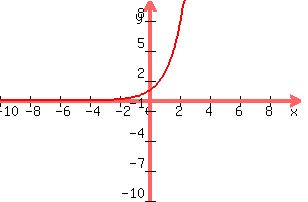
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2C2.7183%5Ex%29
This is the first fastest.
:
f%28x%29=3x-2 This is linear, because x is raised to the first power.
f%281%29=3%281%29-2
f%281%29=1 Plot (1,1)
f%282%29=3%282%29-2
f%282%29=4 Plot (2,4)
f%2816%29=3%2816%29-2
f%2816%29=46
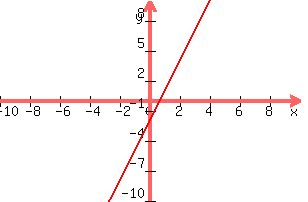
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2C3x-2%29
This is the fourth fastest.
:
f%28x%29=log%28x%29 This is logarithmic because it's a log function.
f%281%29=log%281%29=0 Plot(1,0)
f%282%29=log%282%29=.30103 Plot (2,.3)
f%2816%29=1.2041 Plot (16, 1.2)
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2Cln%28x%29%2Fln%2810%29%29 I figured out how to get it to graph this using ln's and the change of base. Now you can see it.
This is the slowest growing, the fifth fastest.
:
f%28x%29=x%5E2-5x%2B6 This is quadratic because the leading term is raised to the second power.
f%281%29=%281%29%5E2-5%281%29%2B6
f%281%29=2 Plot(1,2)
f%282%29=%282%29%5E2-5%282%29%2B6
f%282%29=0 Plot (2,0)
f%2816%29=182
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2C300%2C200%2Cx%5E2-5x%2B6%29
This is the third fastest.
I'll let you have the fun of the finishing touches.
Happy Calculating!!!