Question 599432: If a stone is thrown upward from a height of 8.25 feet with an initial velocity of 64 feet per second, how long does it take for the stone to fall to the ground? Give answer to the nearest one-hundredth. (Formulas: ; where h represents final height, is initial velocity, t is time and is the initial height)
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a stone is thrown upward from a height of 8.25 feet with an initial velocity of 64 feet per second, how long does it take for the stone to fall to the ground? Give answer to the nearest one-hundredth. (Formulas: ; where h represents final height, is initial velocity, t is time and is the initial height)
.
General formula:
h(t) = -32t^2 + vt + Ho
where
h(t) is height at time t
t is time (secs)
v is initial velocity
Ho is the initial height
.
From stated problem, then, we have:
h(t) = -32t^2 + 64t + 8.25 (formula)
.
how long does it take for the stone to fall to the ground?
set h(t) to zero and solve for t:
h(t) = -32t^2 + 64t + 8.25
0 = -32t^2 + 64t + 8.25
applying the quadratic formula, we get
t = {-0.12, 2.12}
we can throw out the negative solution (extraneous) leaving:
t = 2.12 seconds
.
Details of quadratic to follow:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=5152 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 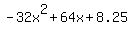 can be factored: can be factored:

Again, the answer is: -0.121522402807898, 2.1215224028079.
Here's your graph:
 |
|
|
|