Question 598754: 1.'A' works twice as fast as 'B'. If both of them together take 6 days to complete the work, in how many days can 'B' alone complete the same?
2.If 10 people working 8 hours a day, can complete a task in 24 days, how many people working 10 hours a day would be required to complete the same task in 16 days?
3.’A’ alone can do a job in 25 days. He worked for 15 days and left. ‘B’ completed the remaining job in 10 days. If both of them work together after initial 15 days in how many more days would the job have been completed?
4.If 10 men can complete a piece of work in 30 days how many men are requiredto complete the same job in 25 days?
5.10men can complete a work in 18 days. After 6 days 5 more men joined. In how many days the remaining work would be completed?
Found 2 solutions by josmiceli, vvnrichards:
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! (1)
You add the individual rates of working to get
the rate of working together
Let A's rate = 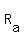
Let B's rate = 
Working together their rate is ( 1 job ) / ( 6 days )
given:


By substitution:



B can finish the job in 18 days working alone
check:







OK
---------
(2)
10 people working 8 hours a day, can complete a task in 24 days
To finish in 1/3 of that time, each person works 3 times longer hours
10 people working 24 hours a day take 8 days
10 people working 12 hours a day take 16 days
120 people working 1 hour a day take 16 days
12 people working 10 hours a day take 16 days
---------
(3)
What fraction of the job does A do in 15 days?
His rate is ( 1 job ) / ( 25 days ), so
fraction = 
That means 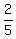 of the job is left of the job is left
‘B’ completed the remaining job in 10 days
Let  = B's rate of working = B's rate of working



With both working together after the initial 15 days,
 = rate woking together = rate woking together


Let  = days to finish working together = days to finish working together



The job will be completed in 5 more days or 20 days altogether
------------
(4)
If 10 men take 30 days,
then 60 men take 5 days
then 12 men take 25 days
( 1/5 as many men take 5 times longer )
------------
(5)
10men can complete a work in 18 days
In 1/3 of that time, 1/3 of the job gets done
so, after 6 days, 2/3 of the job is left
Now 5 men must do 2/3 of the job
If 10men can complete a work in 18 days,
5 men take 36 days to the job
To do 2/3 of a job,
number of days = 
The remaining work is completed in 24 days
------------
Answer by vvnrichards(3)   (Show Source): (Show Source):
|
|
|