Question 598634: Can someone please show me what would a graph look like with the following functions and what are the differences of the letters: Thank you for all of your help!
g(x) = - √x
h(x) = √(x+3)
i(x)= √(x-1)+ 2
j(x) = √(x)+3
Found 2 solutions by stanbon, lwsshak3:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can someone please show me what would a graph look like with the following functions and what are the differences of the letters: Thank you for all of your help!
g(x) = - √x
h(x) = √(x+3)
i(x)= √(x-1)+ 2
j(x) = √(x)+3
---------------------
Comment: Keep in mind that f,g,h,i, and j are all statements about
the y-values in the graph.
------------------------------------
Assume that f(x) = sqrt(x) is the basic graph.
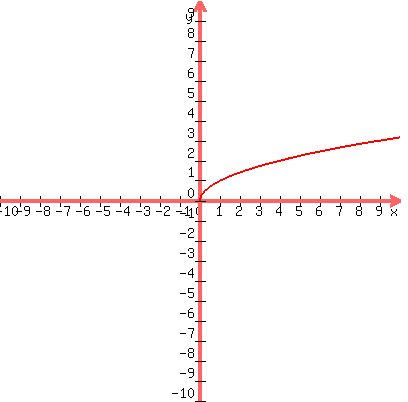
-------------------
g(x) flips f(x) over the y-axis
h(x) moves f(x) 3 units to the left
i(x) moves f(x) 1 unit to the right and raises all the points 2 units
j(x) raises all the points of f(x) 3 units.
=================================
Cheers,
Stan H.
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can someone please show me what would a graph look like with the following functions and what are the differences of the letters: Thank you for all of your help!
g(x) = - √x
h(x) = √(x+3)
i(x)= √(x-1)+ 2
j(x) = √(x)+3
**
Before starting let me add one additional function which will help to explain differences:
f(x)=√x
This is your basic sqrt curve which starts from the origin and gradually increases in the positive direction to infinity.
Domain:[0,∞)
Range: [0,∞)
..
g(x) = - √x
Mirror image of f(x)=√x previously described
Domain:[0,∞)
Range: (∞,0]
..
h(x) = √(x+3)
Moves the basic curve 3 units left. (subtract 3 units from x-coordinates)
Domain:[-3,∞)
Range: (0,∞]
..
i(x)= √(x-1)+ 2
Move basic curve 1 unit right and bumps curve up 2 units. (add 1 unit to x-coordinatess and 2 units to y-coordinates)
Domain:[1,∞)
Range: (2,∞)
..
j(x) = √(x)+3
Bumps basic curve up 3 units (add 3 units to y-coordinates)
Domain:[0,∞)
Range: [3,∞)
|
|
|