Question 59822: can you please help me with this word problem. thank you very much
112. Swimming pool design. An architect has a designed a motel pool with in a rectangular area the is fenced on three sides. If she uses 60 yards of fencing to enclose as area of 352 square yards, then what are the dimensions for L and W? Assume L is greater than W
Found 2 solutions by checkley71, joyofmath:
Answer by checkley71(8403)   (Show Source): (Show Source):
You can put this solution on YOUR website! L*W=352
2L+W=60
W=60-2L
L(60-2L)=352
60L-2L^2-352=0
-2L^2+60L-352=0
L^2-30L+176=0
(L-22)(L-8)=0
L-22=0
L=22 SOLUTION
L-8=0
L=8 SOLUTION
22*W=352
W=352/22
W=16 SOLUTION
PROOF
2*22+16=60
44+16=60
60=60
Answer by joyofmath(189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the width of the pool = W and the length of the pool = L. We are told that the length is greater than W so 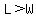 . .
Assume the three sides that are fenced in are the two widths and one length, and that's with 60 yards of fencing. Thus,
(1) 
We also know that the area of the pool = 352. So,
(2) 
Subtract 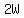 from both sides of (1) to get from both sides of (1) to get 
Replace L with 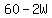 in (2) to get in (2) to get
(3) 
Now, multiply 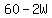 by W and we get by W and we get 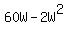 . .
So, (3) becomes  or or
(4) 
This is a quadratic equation which can also be written as  . .
We divide both sides by 2 and get  . .
The coefficients of this quadratic equation are -1, 30, and -176.
Remember the quadratic equation, solving for w: 
Replace a, b, and c with -1, 30, and -176 respectively and you get

Multiply things out and you get
 or or

 so so 
So, W can equal 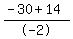 which = 8 which = 8
or W can equal  which = 22 which = 22
From (1) we know that  . If W = 8 then . If W = 8 then  or or  so so  . .
If W = 22 then  or or  or or  so so  . But, L must be > W and 16 is not > 22 so W = 22 is not a solution. . But, L must be > W and 16 is not > 22 so W = 22 is not a solution.
So, L = 44. and from (1) we know that  so so  so so  and and  . .
To verify our answer, that  and and  we plug these values into (1) and (2): we plug these values into (1) and (2):
 so so 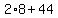 should = 60 and it does. should = 60 and it does.
 so so 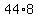 should = 352 and it does. should = 352 and it does.
|
|
|