Question 598048: please help me solve this equation using the means and extremes. factor this. 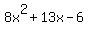
Found 2 solutions by KMST, Alan3354:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The expression "means and extremes" is new to me, but it may be a name for a factoring trick that high school tried to teach my youngest son, so I will show you that.
THE TRICK:
You take the coefficients at both ends and multiply them, as in

(you do not need to worry about negative signs).
Then, you look for pairs factors of that product number. For 48, you find:





Next, you find the pair of factors whose sum or difference is equal to the coefficient of x (13 in your case). You use difference if the independent term is negative, as the -6 in your polynomial.
In this case, I try to get 13 by doing



I wrote them all out, but you would do these calculations in your head (or on scrap paper), and do as few as possible.
For the next step, you draw a large tic-tac-toe grid and enter 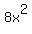 in the center and in the center and  in the bottom right space. Enter in the bottom right space. Enter 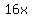 and and 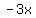 in the spaces in between the in the spaces in between the 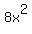 and and  filling a 2X2 square. filling a 2X2 square.
 (It really does not matter in what corner you place the (It really does not matter in what corner you place the 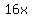 and the and the 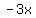 . I could swap their places, and it would work just as well). . I could swap their places, and it would work just as well).
In the spaces above and to the left of those you filled, write the greatest common factor for the row or column.
You are making a multiplication table, where the expressions you already entered are the product of the expressions at the head of the corresponding row and column.

You would get 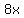 as the greatest common factor for as the greatest common factor for 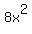 and and 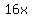 . .
You would get  as the greatest common factor for as the greatest common factor for 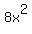 and and 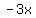 . .
You would get  as the greatest common factor for as the greatest common factor for  and and 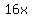 , ,
and that would leave  as the greatest common factor for as the greatest common factor for  and and 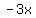 . .
The expressions in the first row are one of your factors.
The expressions in the first column are the other factor.
Your factors are

THE RATIONALE:
If a quadratic trinomial in x (such as the 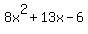 polynomial in your problem) can be factored into something of the form polynomial in your problem) can be factored into something of the form
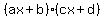 with integer coefficients a, b, c, and d, with integer coefficients a, b, c, and d,
 so the coefficient of the term in x, in the middle of the polynomial, so the coefficient of the term in x, in the middle of the polynomial,
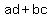 , can be written as the sum of two numbers whose product is , can be written as the sum of two numbers whose product is
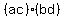 , which is the product of the other two coefficients, the coefficient of , which is the product of the other two coefficients, the coefficient of  , , 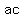 , and the independent term or constant, , and the independent term or constant,  . .
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! please help me solve this equation using the means and extremes. factor this. 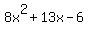
-------------
That's not an equation.
I know, because there's no equal sign.
|
|
|