Question 596587: 4x^5-28x^4-11x^3+77x^2-3x+21 can you help me figure out the zeros?
what would be the graph to determine which of the possibilities?
Express p(X) in completely factored form
Solve algebraically
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The commonly taught techniques of factoring are:- Greatest Common Factor (GCF)
- Factoring patterns:
   - a^3+b^3 = (a+b)(a^2-ab+b^2)
- a^3-b^3 = (a-b)(a^2+ab+b^2)
- Factoring by grouping
- Factoring by trial and error of the possible rational roots
The GCF of your expression is 1 (which we rarely factor out). Your expression has too many terms for either the patterns or for trinomial factoring. So we are left with factoring by grouping and with trial and error of the possible rational roots. Either one of these will work. I'll show you both.
Your expression is not easily factored by grouping. In fact I didn't see it at first myself. Factoring by grouping sometimes requires re-ordering the terms. So I like to start by changing any subtractions into equivalent additions so the terms can be freely re-ordered and re-grouped:

When factoring by grouping you want to create two sub-expressions which each have a GCF within themselves. The grouping that works (and it can take a while to see this) is the one where the terms with a factor of 7 are grouped together and the ones without a factor of 7 are grouped together:

Now we factor out the GCF of each group:

As you can see, the "non-GCF" factors of each sub-expression match. This is what you are looking for. (Note that I factored out -7 instead of 7 from the second sub-expression. But if I did factor out a 7 the "non-GCF" factors would not match. When factoring out GCF's from the sub-expressions, keep in mind factoring out -GCF because this might the right way (like here).)
Now we factor out the "non-GCF" factors:

Before I finish factoring this, I'd like to show you how to get the factoring started with the trial and error method. For any polynomial all the possible rational roots will come from all the ratios, positive and negative, that can be formed using a factor of the constant (at the end) over a factor of the leading coefficient. Your constant term is -21 and your leading coefficient is 4 so the only possible rational roots are 1/1, -1/1, 3/1, -3/1, 7/1, -7/1, 1/2, -1/2, 3/2, -3/2, 7/2, -7/2, 1/4, -1/4, 3/4, -3/4, 7/4 and -7/4. The first six simplify to integers: 1, -1, 3, -3, 7 and -7. 18 possible rational roots is a lot to check. This is why I consider this method the method of last resort (unless the list of possible roots is very short).
Checking the fractions is tedious so I start with the integers. Checking 1 can be done mentally since all the different powers of 1 are still a 1. Trying P(1) we find that it is not zero. -1 is not quite as easy (the even powers are 1 and the odd powers are -1) but it, too, can be done mentally. -1 does not work either. The other possible roots are best checked, IMHO, using synthetic division. I'll try 3 next:
3 | 4 -28 -11 77 -3 21
--- 12 -48 -177 -300 -909
----------------------------------
4 -16 -59 -100 -303 -888
The number is the lower right is the remainder. It is also P(3). Since it is not zero, 3 is not a root. (With P(3), -888, being so far away from zero, it is unlikely that "nearby" possible roots, like 7/2, will work either.) I'll try 7 next:
7 | 4 -28 -11 77 -3 21
--- 28 0 -77 0 -21
----------------------------------
4 0 -11 0 -3 0
The P(7) is zero so...- 7 is a zero
- (x-7) is a factor of P(x); and
- the other factor can be found in the rest of the bottom row. The "4 0 -11 0 -3"" translates into
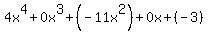 which simplifies to: which simplifies to: 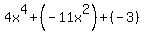
So with either method we get:

Next we factor the first factor. Because the first exponent is twice the exponent in the middle, this expression is in what is called "quadratic form". If you have trouble seeing this, then a temporary variable can help.
Let 
Then 
Substituting these into 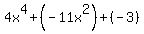 we get: we get:
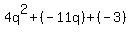
This is obviously a quadratic. And it will factor, using Trinomial factoring, into:
(4q + 1)(q - 3)
Replacing the q's (it was, after all, just a temporary variable) we get:
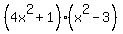
Note: If not now you will eventually see how to go straight from
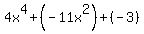
to
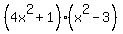
without having to use temporary variables.
Now we have

None of these factors will factor any further so this is the fully factored form.
To find the zeros, we find what value(s) for x make each factor equal to zero. In other words we solve:
 or or  or x - 7 - 0 or x - 7 - 0
Solving each of these we find...
 has no solutions. (After all, how do you square a number, multiply it by 4 and end up with zero. Answer: You can't *unless complex numbers are allowed. Think about it.) has no solutions. (After all, how do you square a number, multiply it by 4 and end up with zero. Answer: You can't *unless complex numbers are allowed. Think about it.)
The solutions to  are: are:
 or or 
And the solution to x - 7 = 0 is
x - 7
So the real zeros to P(x) are,  , ,  and 7. and 7.
I'm not sure what you mean by "what would be the graph to determine which of the possibilities" so I can't help you there except to say that the zeros of P(x) represent the only x-intercepts on the graph of P(x).
|
|
|