2x - 3y - z = 0
3x + 2y + 2z = 2
x + 5y + 3z = 2
I will assume you have had matrices. If not,
post again and I will show you how to solve
it without matrices:
The augmented matrix is
[2 -3 -1 | 0]
[3 2 2 | 2]
[1 5 3 | 2]
We need to get 0's in the three lower left
positions, that is, in the positions below
the upper left to lower-right diagonal:
To get a 0 where the 3 in row 2 column 1 is,
we multiply row 1 temporarily by -3 and add it
to 2 times row 2. This is easy to do mentally
if you write -3 to the left of row 1 and 2 left
of row 2:
-3[2 -3 -1 | 0]
2[3 2 2 | 2]
[1 5 3 | 2]
[2 -3 -1 | 0]
[0 13 7 | 4]
[1 5 3 | 2]
To get a 0 where the 1 in row 3 column 1 is,
we multiply row 1 temporarily by -1 and add it
to 2 times row 3. This is easy to do mentally
if you write -1 to the left of row 1 and 2 left
of row 3:
-1[2 -3 -1 | 0]
[0 13 7 | 4]
2[1 5 3 | 2]
[2 -3 -1 | 0]
[0 13 7 | 4]
[0 13 7 | 4]
To get a 0 where the 13 in row 3 column 2 is,
we multiply row 2 temporarily by -1 and add it
to 1 times row 3. This is easy to do mentally
if you write -1 to the left of row 2 and 1 left
of row 3:
-1[2 -3 -1 | 0]
[0 13 7 | 4]
2[0 13 7 | 4]
[2 -3 -1 | 0]
[0 13 7 | 4]
[0 0 0 | 0]
Now that we have the three zeros,
the above is the abbreviation of this system:
2x - 3y - 1z = 0
0x + 13y + 7z = 4
0x + 0y + 0z = 0
or
2x - 3y - z = 0
13y + 7z = 4
0z = 0
The bottom equation,
0z = 0
has as a solution "z can equal to any real number"
So we can select any letter to stand for any real number,
say the letter k.
So z = k
We substitute k for z into the middle equation
13y + 7z = 4
13y + 7k = 4
13y = 4 - 7k
y = 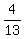 -
- 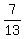 k
We substitute k for z and
k
We substitute k for z and 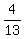 -
-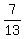 k for y into
the top equation:
2x - 3y - z = 0
2x - 3(
k for y into
the top equation:
2x - 3y - z = 0
2x - 3(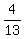 -
-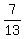 k) - k = 0
2x - (
k) - k = 0
2x - ( +
+ 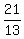 k) - k = 0
Clear of fractions by multiplying through by 13:
26x - 12 + 21k - 13k = 0
26x - 12 + 8k = 0
26x = 12 - 8k
x =
k) - k = 0
Clear of fractions by multiplying through by 13:
26x - 12 + 21k - 13k = 0
26x - 12 + 8k = 0
26x = 12 - 8k
x =  -
- 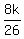 x =
x = 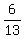 -
- 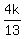 Solution:
(x, y, z) = (
Solution:
(x, y, z) = (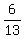 -
-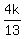 ,
, 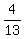 -
-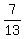 k, k)
Edwin
k, k)
Edwin