SOLUTION: The period T (in seconds) of a pendulum can be modeled by (T= 1.11 to the square root of l) where l is the pendulum's length (in feet). A) How long is a pendulum with a period of

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: The period T (in seconds) of a pendulum can be modeled by (T= 1.11 to the square root of l) where l is the pendulum's length (in feet). A) How long is a pendulum with a period of      Log On


   

Question 596093: The period T (in seconds) of a pendulum can be modeled by (T= 1.11 to the square root of l) where l is the pendulum's length (in feet).
A) How long is a pendulum with a period of 5 seconds?
B) What is the length of the pendulum with a time period of 1.4 seconds?
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
(Note: Since "l" looks so much like "1", I am going to use an uppercase l: "L")
T+=+1.11%5Esqrt%28L%29
a) Find L when T = 5.
5+=+1.11%5Esqrt%28L%29
Now we solve for l. (Since solving for a variable that is in an exponent usually involves logarithms, I have reclassified this as a logarithm problem.)

Here's a general procedure for solving for a variable that is in an exponent:
  1. Isolate the base and its exponent.
  2. Find the logarithm of each side. Any base of logarithm may be used. But there are advantages to choosing certain ones:
    • If the base of the logarithm matches the base of the exponent, then your answer will be s simpler expression.
    • If the base of the logarithm is 10 or e (i.e. common or natural logarithms), then the answer will have logarithms a calculator can find (in case you want or need a decimal approximation for the answer.
  3. Use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to "move" the exponent of the log's argument out in front of the log.
  4. With the variable now out of an exponent, you have an equation which should be solvable for that variable.

Let's see how this works on
5+=+1.11%5Esqrt%28L%29
1. Isolate the base and its exponent. In this equation there are not extra terms on the right side and there are no coefficients in front of the base. IOW, the base and exponent are already isolated.

2. Find the logarithm of each side. Any base of logarithm may be chosen. But base 1.11 (because it matches the base of 1.11%5E%28sqrt%28L%29%29, base 10 or base e (ln) are best. (I will use base 1.11 right now. Later I will do it again with base e so you can see the difference.)
log%281.11%2C+%285%29%29+=+log%281.11%2C+%281.11%5Esqrt%28L%29%29%29

3. Move the exponent out in front:
log%281.11%2C+%285%29%29+=+sqrt%28L%29%2Alog%281.11%2C+%281.11%29%29
Since log%28a%2C+%28a%29%29+=+1 for every base, the log on the right side simplifies to a 1. (This is why matching the base of the log to the base of the exponent results in a simpler expression.) So now we have:
log%281.11%2C+%285%29%29+=+sqrt%28L%29

4. Solve the equation (now that the variable is out of an exponent). Squaring both sides we get:
%28log%281.11%2C+%285%29%29%29%5E2+=+L
This is an exact expression for the answer to this problem. If you want or need a decimal approximation, then
  • Use the change of base formula to convert the base 1.11 log into base 10 or base e logs; or
  • you should have shosen base 10 or base e logs instead of base 1.11.
Let's see how this would have worked out with base e logs. (Since the logic of the steps is the same, I will only comment on the differences.)
5+=+1.11%5Esqrt%28L%29
ln%285%29+=+ln%281.11%5Esqrt%28L%29%29
ln%285%29+=+sqrt%28L%29%2Aln%281.11%29
(Note how the log on the right does not disappear this time.) Divide both sides by ln(1.11):
ln%285%29%2Fln%281.11%29+=+sqrt%28L%29
%28ln%285%29%2Fln%281.11%29%29%5E2+=+L
This is another exact expression for the answer. It is not as simple as when we used base 1.11 logs but a calculator can turn this one into a decimal approximation.

If you want a decimal, I'll leave that up to you.

b. Find L when T = 1.4
1.4+=+1.11%5Esqrt%28L%29
log%281.11%2C+%281.4%29%29+=+log%281.11%2C+%281.11%5Esqrt%28L%29%29%29
log%281.11%2C+%281.4%29%29+=+sqrt%28L%29%2Alog%281.11%2C+%281.11%29%29
log%281.11%2C+%281.4%29%29+=+sqrt%28L%29
%28log%281.11%2C+%281.4%29%29%29%5E2+=+L
Using base e:
%28ln%281.4%29%2Fln%281.11%29%29%5E2+=+L
Using base 10:
%28log%28%281.4%29%29%2Flog%28%281.11%29%29%29%5E2+=+L

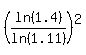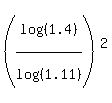If you're not convinced that the base of the logarithm does not matter, then I suggest that you get decimal approximations for %28ln%281.4%29%2Fln%281.11%29%29%5E2 and %28log%28%281.4%29%29%2Flog%28%281.11%29%29%29%5E2and compare them.