SOLUTION: Find a polynomial of minimum degree that has the given zeros: {{{11-sqrt(3)}}} and {{{11+sqrt(3)}}}. . The polynomial is:

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Find a polynomial of minimum degree that has the given zeros: {{{11-sqrt(3)}}} and {{{11+sqrt(3)}}}. . The polynomial is:      Log On


   

Question 596017: Find a polynomial of minimum degree that has the given zeros: 11-sqrt%283%29 and 11%2Bsqrt%283%29.
.
The polynomial is:
Found 2 solutions by math-vortex, richard1234:
Answer by math-vortex(648) About Me  (Show Source):
You can put this solution on YOUR website!
Find a polynomial of minimum degree that has the given zeros.
11-sqrt%283%29 and 11%2Bsqrt%283%29.
Hi, there--
.
Since we have two zeros here, the degree of the polynomial will be two at a minimum. In addition, every root corresponds to a factor of the polynomial. To find a polynomial, we take each root and turn it into a factor. Then, we multiply the factors together to give the polynomial. Let's write the polynomial in terms of x.
.
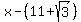If 11-sqrt%283%29 is a zero for our polynomial, then x-%2811-sqrt%283%29%29 is a factor. Likewise, if 11%2Bsqrt%283%29 is a zero for our polynomial, then x-%2811%2Bsqrt%283%29%29 is the other factor.
.
So, our polynomial in factored form is
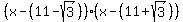
%28x-%2811-sqrt%283%29%29%29%28x-%2811%2Bsqrt%283%29%29%29
.
We'll simplify, multiply this out using the distributive property, and combine like terms to get the polynomial into expanded form.
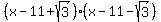
%28x-11%2Bsqrt%283%29%29%28x-11-sqrt%283%29%29

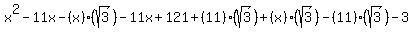
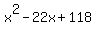
x%5E2-22x%2B118
.
I hope this helps! Feel free to email if any part of my explanation is unclear.
.
Ms.Figgy
math.in.the.vortex@gmail.com

Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!


We can also write this as



Applying the difference of two squares, this is equal to