SOLUTION: Use synthetic division to divide the polynomial (2x^3+11x^2-2x-25) divided by the linear factor (2x+3) and state in the from Q(x)+r(x) where r(x) is the remainder.

Synthetic division is only for division by x-r, where the coefficient
of x is 1.  So to use synthetic division when the coefficient of x
is not 1, you must first write the division as a fraction:



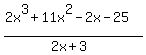Then factor out the coefficient x, in this case 2, in the bottom

(Yes I know you were taught that you couldn't factor anything out of
2x+3, but they meant that you couldn't factor anything out of it without
running into fractions, but you're a big boy or girl now :) and you
can handle fractions.  So factor out 2, and get 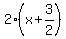 and put
up with a fraction inside the parentheses: 



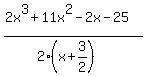Now consider that coefficient 2 you factored out on the boottom 
as amounting to multiplication by the fraction : 

×

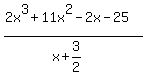We will do the fraction by synthetic division and 
then divide through by 2

-⃒ 2  11  -2  -25
  ⃒    -3 -12   21  
    2   8 -14   -4

This quotient is 2x² + 8x - 14 +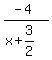 

Then we multiply by 1/2 and get:

        x² + 4x - 7 +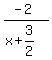  

We can simplify the fraction by multiplying top and bottom
by 2

        x² + 4x - 7 + 

And then we can just put a minus sign and make the numerator 4

        x² + 4x - 7 - 

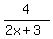Edwin