Question 59581: I can't seem to get these right - help would be appreciated:
(Not necessary to find the roots - just determine the number & type of solution) use a discriminant to determine the number of solutions for the quadratic equasions - and if the solutions are real or complex.
a. 2x^2+x-1=0
b. 4/3x^2-2x+3/4=0
c. m^2+m+1=0
Thank you very much!
Found 3 solutions by stanbon, uma, funmath:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! a. 2x^2+x-1=0
discrim=1^2-4*2*-1=9; 2 real zeroes
---------------
b. 4/3x^2-2x+3/4=0
multiply thru by 12 to get:
16x^2-24x+9=0
discrim= 24^2-4*16*9=0; 2 identical real zeroes
--------------
c. m^2+m+1=0
discrim=1^2-4*1*1=-3 ; 2 complex zeroes.
-------------
Cheers,
Stan H.
Answer by uma(370) (Show Source):
You can put this solution on YOUR website! 1. 2x^2 + x - 1 = 0
Here a = 2, b = 1 and c = -1
Discriminant D = b^2 - 4ac
= 1^2 - 4(2)(-1)
= 1 +8
= 9
9 is positive and a perfect square.
So the two roots of the given equation are real and rational.
b) 4/3 x^2 -2x + 3/4 = 0
Here a = 4/3, b= -2 and c= 3/4
Discriminant = D = b^2 - 4ac
= (-2)^2 - 4(4/3)(3/4)
= 4 - 4
= 0
As the discriminant is zero, the given equation has two real and equal roots.
c) m^2 + m + 1 = 0
Here a = 1, b = 1 and c = 1.
Discriminant = D = b^2 - 4ac
= 1^2 - 4(1)(1)
= 1 - 4
= -3
D is negative and so both the roots of the given equation are complex.
Good Luck!!!
Answer by funmath(2933) (Show Source):
You can put this solution on YOUR website! (Not necessary to find the roots - just determine the number & type of solution) use a discriminant to determine the number of solutions for the quadratic equasions - and if the solutions are real or complex.
:
The discriminant of a quadratic equation written in standard form  is 
If the discriminant is positive, there are two real solutions.
If the discriminant is 0, there is one real solution.
If the discriminant is negative, there are two complex solutions.
:
a. 2x^2+x-1=0 a=2, b=1, c=-1
= The discriminant is positive, there are two real solutions.
:
b. 4/3x^2-2x+3/4=0 a=4/3, b=-2, c=3/4
=
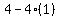
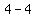
 The discriminant is 0, there is one real solution.
:
c. m^2+m+1=0 a=1, b=1, c=1
=
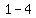
= The discriminant is negative, there are two complex solutions.
:
Happy Calculating!!!
|
|
|
