Question 595782: tan θ − 3 cot θ = 0
Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to three decimal places where appropriate. If there is no solution, enter NO SOLUTION.)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! (Note: To save typing I'm going to use "x" instead of theta. Just replace my x's with theta's. Also, I'm assuming that the problem is using the convention of theta indicating that the angles are expressed in degrees. If this is not true, then multiply any answers below by  to convert them to radian measure.) to convert them to radian measure.)
tan(x) - 3*cot(x) = 0
Solving equations like this often starts by using algebra and/or trig identities to transform it into one or more equations of the form:
TrigFunction(something) = some-number
For example: sin(x) = 0, tan(4x) = 1, etc.
One technique that is often used is to use replace sec, csc, tan and cot (if any) with equivalent expressions of sin and/or cos. (Note: This is no a bad technique but I recommend that you look for other solutions before resorting to this one.) Replacing tan and cot we get:

(Note the use of parentheses. This is an extremely good habit when replacing one expression with another!) At this point we can either subtract the fraction (after getting common denominators first, of course) or we can eliminate the fractions. I prefer eliminating the fractions. To do so, we multiply each side of the equation by the LCD (which is sin(x)*cos(x)):

which simplifies to:

Since the sin's and cos's are squared, we can use one of the Pythagorean identities to turn the sin into cos (or vice versa). Replacing  with with 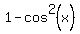 we get: we get:

Simplifying we get:

By making the substitutions we have made we have transformed the equation into one that has a single trig function, cos, with a single argument. We should be able to solve an equation in this form. If you look closely you can will recognize that- One side of the equation is zero
- The other side is a difference of squares and, therefore, it will factor.

Now we can use the Zero Product Property which tells us that one of these factors must be zero. So:
1 + 2*cos(x) = 0 or 1 - 2*cos(x)
Solving these we get:
cos(x) = -1/2 or cos(x) = 1/2
We now have transformed the original equation into two equations of the desired form.
Angles whose cos is 1/2 (and -1/2) are special angles so we shold know what these angles are. For cos(x) 1/2 we should get:
x = 60 + 360k or x = -60 + 360k
For cos(x) = -1/2 we should get:
x = 120 + 360k or x = 240 + 360k
Note: Since the original equation had tan and cot and since these functions are undefined for certain angles, you must check your solution and reject any angles that would make either of these functions undefined. When we check we will find that both tan and cot are defined for 60, -60, 120, 240. So we do not have to reject any part of our solution.
This makes the general solution:
x = 60 + 360k or x = -60 + 360k or x = 120 + 360k or x = 240 + 360k
|
|
|