SOLUTION: if the average of x, y, and 35 is 20 less than the average of y, z, and 100, what is the value of x-z?

Algebra ->  Average -> SOLUTION: if the average of x, y, and 35 is 20 less than the average of y, z, and 100, what is the value of x-z?      Log On


   

Question 595500: if the average of x, y, and 35 is 20 less than the average of y, z, and 100, what is the value of x-z?
Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
if the average of x, y, and 35 is 20 less than the average of y, z, and 100,
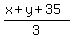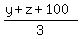%28x%2By%2B35%29%2F3 = %28y%2Bz%2B100%29%2F3 - 20
multiply eq by 3, results
x + y + 35 = y + z + 100 - 60
x + y + 35 = y + z + 40
x + y = y + z + 40 - 35
x + y = y + z + 5
Subtract y from both sides
x = z + 5
Subtract z from both sides
x - z = 5