Question 594929: Hi! I'm having trouble with this word problem about compound interest and logs:
Annie invests $1000 at an interest rate of 10% compounded anually. Deena invests $1500 at a interest rate of 5% compounded annually. After how many years will they have accumulated the same amount?
I wrote out the equation like this but do not know how to solve it:
Please help!!!
Found 2 solutions by scott8148, jsmallt9:
Answer by scott8148(6628)   (Show Source):
You can put this solution on YOUR website! dividing by 1000 ___ 1.1^x = 1.5 * 1.05^x
taking log ___ x * log(1.1) = log(1.5) + x * log(1.05)
subtracting [x * log(1.05)] ___ [x * log(1.1)] - [x * log(1.05)] = log(1.5)
factoring ___ x {[log(1.1)][log(1.05)]} = log(1.5)
dividing by {[log(1.1)][log(1.05)]} ___ x = log(1.5) / {[log(1.1)][log(1.05)]}
logs are on "scientific" calculators (there's one built into Windows), or in a table in a book
Answer by jsmallt9(3758)  (Show Source):
You can put this solution on YOUR website!
It is often good to start by simplifying. Let's add the numbers in the parentheses:
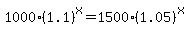
Next we can reduce the numbers by dividing both sides by 1000:
Now we will find the logarithm of each side. Any base of logarithm can be used but if you want a decimal approximation of the answer, then it would be best to choose a base your calculator "knows", base 10 or base e (ln). I'll use ln:
For reasons you will soon see, we must use a property of logarithms,  to split the log on the right:
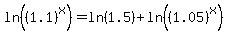
Now we use a property of logarithms,  , to move the exponents in the first and last logs out in front of each log. (This property is the very reason we use logarithms on equations like this. It allows us to bring the exponent, where the variable is, "down to earth" where we can use regular algebra to solve for it.) Note: We could use this property on ln(1.5(1.05)^x) because the exponent is just on the 1.05, not on the entire argument. This is why we split that log in the previous step.
Now that the x's are "out in the open", we solve for x. We'll start with gathering the terms with a variable on one side. Subtracting x*ln(1.05) from each side we get:
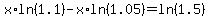
Factoring out x we get:
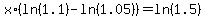
Dividing by (ln(1.1) - ln(1.05)) we get:
This is an exact expression for the solution and it may be acceptable in this form. But we can do a little more simplifying. We can use  to combine the logs in the denominator:
Dividing out the fraction in the log in the denominator we get:
And, since the right side matches the pattern of the right side of the change of base formula,  , we could simplify this even further:
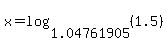
In summary, we have three exact expressions for the answer:
I'll let you decide which one to use. (The third one is simplest but the other two have the advantage that you can use a calculator to find a decimal approximation if needed or wanted.)
|
|
|
