Select any two integers between -12 and +12 which will become solutions to a system of two equations.
I choose arbitrarily x=4 and y=-7 so that (x,y) = (4,-7) will
become solutions to a system I will create.
Write two equations that have your two integers as solutions.
Show how you built the equations using your integers.
Create the first equation that has solution (x,y) = (4,-7):
Arbitrarily choose two numbers for coefficients for
x and y. I arbitrarily choose 3 and -2 and write the
left side of the first equation using those two coefficients
I chose, followed by an equal sign:
3x - 2y =
Now substitute 4 for x and -7 for y:
3(4) - 2(-7) =
12 + 14 =
26
Write 26 after the = sign:
3x - 2y = 26
That is the first equation that has solution (x,y) = (4,-7)
Now make a second equation that has solution (x,y) = (4,-7):
Arbitrarily choose two other numbers for coefficients for
x and y. I arbitrarily choose 4 and 3 this time and write the
left side of the first equation with those two coefficients
I chose, followed by an equal sign:
4x + 3y =
Now substitute 4 for x and -7 for y:
4(4) + 3(-7) =
16 - 21 =
-5
Write -5 after the = sign:
4x + 3y = -5
That is the second equation that has solution (x,y) = (4,-7)
Solve your system of equations by the addition/subtraction method. Make sure you show the necessary 5 steps.
3x - 2y = 26
4x + 3y = -5
Step 1: Eliminate y by multiplying the first equation through by 3
and the second equation through by 2:
9x - 6y = 78
8x + 6y = -10
Step 2: Add the two equations term by term:
9x - 6y = 78
8x + 6y = -10
---------------
17x = 68
Step 3: Solve for x
x = 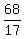 x = 4
Step 4: Susbtitute 4 for x in one of the two original equations,
I choose the first one:
3x - 2y = 26
3(4) - 2y = 26
Step 5: Solve for y:
12 - 2y = 26
-2y = 14
y =
x = 4
Step 4: Susbtitute 4 for x in one of the two original equations,
I choose the first one:
3x - 2y = 26
3(4) - 2y = 26
Step 5: Solve for y:
12 - 2y = 26
-2y = 14
y =  y = -7
Solution (x,y) = (4,-7)
Edwin
y = -7
Solution (x,y) = (4,-7)
Edwin