Question 594339: simplify
square root of 637/144 (the whole fraction is inside the sqaure root box)
a. 637/144
b. 7(square root 13)/144
c. 7(square rrot 13)/12
d. 91/12
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are asked to simplify:
.
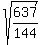
.
If it can be simplified, it likely means that there are factors in the numerator or the denominator (or both) that are perfect squares and therefore can be removed from the square root operation.
.
You may be aware that the denominator 144 is equal to 12 squared. So you can substitute 12 squared for 144 to convert the problem to:
.
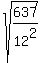
.
But what about the numerator 637? Is it a perfect square, or can it be factored such that one of the factors is a perfect square? 637 is not a perfect square. That's relatively easy to determine. 25 squared is only 625 and therefore 25^2 is too small. And 26 squared is bigger than 637. Therefore, 26 squared is too big. This tells you that unlike the denominator, 637 is not a perfect square.
.
From a testing strategy, you can look at the answers you are given and get a clue about factoring 637. (From your work above with the denominator, you already know that the denominator is the square root of 144, or 12. So answers a and b are not correct. But answers c and d are still possibilities.) Looking at answer c, it appears as if 7 is a candidate as a multiple factor of 637. Using that as a clue will save you some work in factoring 637. So you can start by dividing 637 by 7 and find that the answer is 91. Now divide 91 by 7 and the answer is 13. And 13 is a prime number, so it can't be factored further. You now know that 637 factors into 7 times 7 times 13, or 7 squared times 13.
.
So you have converted the problem to:
.

.
and by the rules of radicals this is equal to:
.

.
The base of each of the squared terms can be removed from its radical as a multiplier as shown below:
.

.
The answer to this problem is c.
.
Hope this helps you understand the problem a little better.
.
|
|
|