Question 594338: square root of 15 times (square root of 45 - square root of 15)
a. 3(square root 75) -15
b. 15(square root3) - 2(square root 15)
c. 15(square root 3) - 15
d. 15(square root 2)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!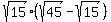 
First simplify the square roots. Then simplify the expression as a whole. And finally, simplify any remaining square roots.
Simplifying square roots is done by finding perfect square factors (4, 9, 16, 25, etc. 1 is a perfect square, too, but 1 is of no use in simplifying square roots) in the radicand. ("Radicand" the the name for the expression inside a radical.) Since 15 does not have any factors that are perfect squares, the first and last square roots will not simplify. But the 45 does have a perfect factor of 9. So we start by factoring that radicand:
Next we use a property of all radicals (including square roots),  , to separate the factors into their own "personal" square roots:
With the perfect square now in its own square root we can replace it with its known value:
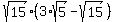
Next we simplify the expression as a whole. The two terms within the parentheses are not like terms so we cannot subtract them. But we can use the Distributive Property to multiply:
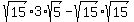
The product at the end should be obvious. To multiply the first product we will multiply the two square roots, using the property listed above in the other direction. (Remember that multiplication is commutative and associative so we can multiply in any order we choose. This is what allows us to ignore the 3 for now and just multiply the square roots.)
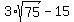
NOTE: This matches answer "a". But we can't just stop here. We must simplify, if possible, the remaining square root. Once again we look for perfect square factors. 25 is a perfect square and it it a factor of 75 so we will be able to simplify that square root:
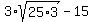
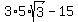
which simplifies to:
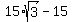
This matches answer "c". ("a" is correct but not fully simplified so it is not the best answer.)
|
|
|
