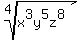Rules for 
1. If M is less than N, then leave it as it is.
2. If M can be divided evenly by N, then it equals
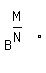
3. If M is greater than N, then do this division
where Q is the quotient and R is the remainder
Q
N)M
...
R
Then it equals:
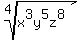For the x³, since 3 is less than 4, we use rule 1 and do nothing
For they y5, since 5 is greater than 4, we use rule 3
and do this division:
1
4)5
4
1
and write:
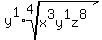and dispose of the 1 exponents:
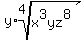For the z8, since 8 can be divided evenly by 4, we
use rule 2 and we end up with
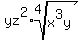Edwin
