y = 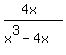 Factor the denominator:
Factor out x in the denominator:
y =
Factor the denominator:
Factor out x in the denominator:
y = 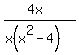 Notice that x is a factor of both the numerator and denominator. In earlier
algebra courses you were told just to cancel the like factors in the numerator
and denominator. However they told you that because they didn't want to get
you too involved in those earlier courses.
What they didn't tell you in those earlier courses is that if you cancel the
like factors in the numerator and denominator, you must NOT INCLUDE on your
graph any point of the resulting equation's graph after canceling them. So
what we do in this course is to cancel, draw the graph, then remove any
point(s) for which the canceled factors equals 0.
First we cancel the x's, but we must not forget that we canceled them as we did
in earlier courses:
y =
Notice that x is a factor of both the numerator and denominator. In earlier
algebra courses you were told just to cancel the like factors in the numerator
and denominator. However they told you that because they didn't want to get
you too involved in those earlier courses.
What they didn't tell you in those earlier courses is that if you cancel the
like factors in the numerator and denominator, you must NOT INCLUDE on your
graph any point of the resulting equation's graph after canceling them. So
what we do in this course is to cancel, draw the graph, then remove any
point(s) for which the canceled factors equals 0.
First we cancel the x's, but we must not forget that we canceled them as we did
in earlier courses:
y = 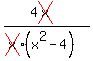 y =
y = 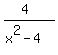 Draw a set of axes:
Draw a set of axes:
 Find the vertical asymptotes:
Set the denominator = 0
x² - 4 = 0
(x - 2)(x + 2) = 0
x - 2 = 0; x + 2 = 0
x = 2; x = -2
So there are two vertical asymptotes:
x = 2 (a vertical line through 2 on the x axis)
x = -2 (a vertical line through -2 on the x axis)
When the degree of the numerator is less than the degree of the denominator,
the horizontal asymptote is the x-axis, whose equation is y=0.
I will color them all the asymptotes green, but on your paper you can draw them
as dotted lines:
Find the vertical asymptotes:
Set the denominator = 0
x² - 4 = 0
(x - 2)(x + 2) = 0
x - 2 = 0; x + 2 = 0
x = 2; x = -2
So there are two vertical asymptotes:
x = 2 (a vertical line through 2 on the x axis)
x = -2 (a vertical line through -2 on the x axis)
When the degree of the numerator is less than the degree of the denominator,
the horizontal asymptote is the x-axis, whose equation is y=0.
I will color them all the asymptotes green, but on your paper you can draw them
as dotted lines:
 We can if we like check for symmetry with respect to the y-axis and origin by
replacing x by (-x), simplifying and seeing whether we get:
1. the original equation, the original equation, which would mean the graph
would be symmetrical with respect to the y-axis.
2. the original equation except with the right side multiplied by -1, which
would mean the graph is symmetrical with respect to the origin.
3. Neither, in which case the graph would not have symmetry with respect to the
y-axis or the origin.
y =
We can if we like check for symmetry with respect to the y-axis and origin by
replacing x by (-x), simplifying and seeing whether we get:
1. the original equation, the original equation, which would mean the graph
would be symmetrical with respect to the y-axis.
2. the original equation except with the right side multiplied by -1, which
would mean the graph is symmetrical with respect to the origin.
3. Neither, in which case the graph would not have symmetry with respect to the
y-axis or the origin.
y =  y =
y =  y =
y =  It came back to the y =
It came back to the y =  , so it is symmetrical with respect to
the y-axis.
So we only need to get a few points on the right left and right of the vertical
asymptote:
x | y
0 | -1
1 | -1.3
1.5 | -2.3
2.5 | 1.8
3 | 0.8
We plot those:
, so it is symmetrical with respect to
the y-axis.
So we only need to get a few points on the right left and right of the vertical
asymptote:
x | y
0 | -1
1 | -1.3
1.5 | -2.3
2.5 | 1.8
3 | 0.8
We plot those:
 Then due to symmetry, match them on the left side of the y-axis:
Then due to symmetry, match them on the left side of the y-axis:
 Draw in the graph:
Draw in the graph:
 But we cannot stop here as we could have in lower courses of algebra, because
the graph of y =
But we cannot stop here as we could have in lower courses of algebra, because
the graph of y =  is NOT quite the same graph as the graph of
y =
is NOT quite the same graph as the graph of
y = 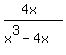 .
We must remove from the graph of y =
.
We must remove from the graph of y =  any point for which the
factor we canceled equals 0. So we must remove the point when x = 0, which is
the point (0,-1).
So the graph of y =
any point for which the
factor we canceled equals 0. So we must remove the point when x = 0, which is
the point (0,-1).
So the graph of y = 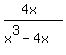 is this
is this
 Notice the circle around the point (0,-1). The graph does not include that
point. So we say "there is a removeable discontinuity at x=0". Colloquially
we say "There is a hole in the graph at x=0".
Edwin
Notice the circle around the point (0,-1). The graph does not include that
point. So we say "there is a removeable discontinuity at x=0". Colloquially
we say "There is a hole in the graph at x=0".
Edwin